Проектирование кулачковых механизмов

Введение

Кулачковые механизмы - плоские или пространственные механизмы с одной высшей кинематической парой, выполняющие самые разные функции, получившие широкое распространение в механизмах перемещения рабочих органов различных машин-автоматов, в устройствах подачи станков, механизмах газораспределения двигателей внутреннего сгорания и во многих других случаях, когда требуется получить возвратно- вращательное или возвратно-поступательное движение ведомого звена по заданному закону. Воспроизведение движения ведомого звена (толкателя) кулачковые механизмы осуществляют теоретически точно. Их ведущее звено называется кулачком.

Кулачковый механизм, в большинстве случаев, является составной частью проектируемой машины. Он может использоваться как основной, но чаще является вспомогательным механизмом для выполнения технологической операции, последовательность и продолжительность которой согласуется с движением звеньев основного механизма.

Поэтому проектирование кулачковых механизмов выполняется после того, как предварительно намечена общая компоновка машины, спроектированы ее рабочие органы, установлена продолжительность и последовательность выполнения элементов движения ведомого звена кулачкового механизма, выбран закон движения.

Проектирование кулачкового механизма заключается в определении взаимного расположения ведущего звена (кулачка), ведомого звена (толкателя) и координат профиля кулачка, обеспечивающих заданный закон движения толкателя. При этом должны быть удовлетворенны требования, определяющиеся технологическим процессом и эксплуатационными показателями механизма. Эти требования отражаются в исходных данных для проектирования.

Проектное решение оценивается комплексом показателей, таких как, размеры, взаимозаменяемость деталей, их прочность, долговечность, стоимость и т.д. Получить решение, в котором все эти показатели являются оптимальными, невозможно. Поэтому оптимизируют один или несколько показателей с обеспечением выполнения ограничений по остальным показателям.
Применение системы автоматизированных расчетов курсового проектирования [1] позволяет рассматривать при проектировании многовариантные решения и выбирать наилучший вариант конструкции.

В данном учебном пособии рассмотрена методика проектирования кулачковых механизмов с оптимизацией по габаритам. Дополнительное условие синтеза - обеспечение допустимых углов давления на входное звено во всех положениях механизма, т.е. обеспечение отсутствия заклинивания кулачкового механизма. Наряду с аналитическим методом, реализованным на ЭВМ в диалоговом режиме, дается и графический.

1. Исходные данные, основные требования и этапы проектирования

В комплексных заданиях на курсовой проект (работу) содержатся следующие исходные данные:

1. Структурная схема кулачкового механизма, показывающая характер взаимосвязей звеньев и их относительное расположение, тип кулачка, вид толкателя и характер его движения. Ведущим звеном в кулачковом механизме (рис. 1, 2) является дисковый кулачок 1, ведомым - толкатель 2, снабженный роликом 3. Толкатель может совершать поступательное (рис. 1) или вращательное (рис. 2) движение.

2. Максимальное перемещение толкателя - ход толкателя h (рис. 1, 2) или угол поворота толкателя b

(рис. 2)

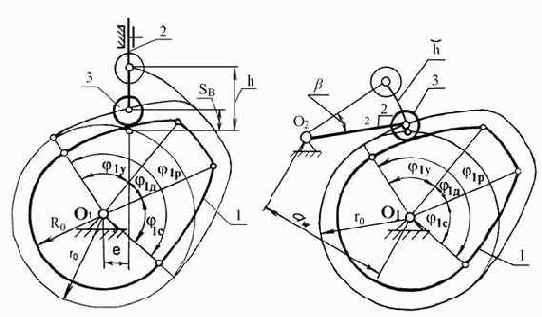
Рис.1 Рис.2

3. Длина толкателя

2 в случае вращательно перемещающегося толкателя или внеосность е в случае поступательно движущегося толкателя.

4. Фазовые углы: угол рабочего профиля кулачка

и его составляющие - при удалении

, при дальнем стоянии

, и сближении

, которые назначаются в соответствии с циклограммой, отражающей согласованность перемещений исполнительных звеньев механизма.

5. Закон движения толкателя в виде графика изменения ускорения толкателя в зависимости от угла поворота кулачка. Закон движения определяется конкретной технологической операцией, для выполнения которой предназначен проектируемый механизм.

6. Допустимый угол давления [J].

7. Направление вращения кулачка и частота его вращения в с-1.

При проектировании кулачковых механизмов необходимо соблюдать следующие основные требования:

проектируемый механизм должен обеспечивать заданный закон движения; механизм должен иметь наименьшие габариты при достаточной надежности работы; детали, составляющие механизм, должны быть технологичными, а их сборка - простой. Проектирование кулачкового механизма делится на три основных этапа:

1. Определение кинематических передаточных функций, характеризующих изменение ускорения, скорости и перемещения толкателя, в функции времени или угла поворота кулачка.

2. Определение основных размеров кулачкового механизма - минимального радиуса кулачка

, внеосности

или межосевого расстояния

w, при которых углы давления не превышают допустимых значений.

3. Определение координат профиля кулачка.

Проектирование кулачкового механизма может быть выполнено графическим методом либо по аналитическим зависимостям с применением ЭВМ. В учебных целях при выполнении курсового проекта используют сочетание графических методов определения параметров кулачкового механизма с анализом математических моделей и выполнением расчетов на ЭВМ.

Применение графического метода позволяет предварительно изучить алгоритм реализации поставленной задачи, выявить связи между отдельными параметрами и сформировать математическую модель для составления программы расчета на ЭВМ. В итоге расчетов на ЭВМ студент получает таблицу результатов, которые ему следует проанализировать и сравнить с результатами графических построений и вычислений.

2. Выбор закона движения толкателя

При проектировании профиля кулачка обычно задаются законом движения толкателя. Выбор закона движения определяется главным образом теми требованиями, которые предъявляет технологический процесс к движению толкателя. В качестве требуемого закона движения можно принять определенный тип кривой перемещения, скорости или ускорения. Динамика кулачковых механизмов в основном определяется законами изменения ускорений (так как с ускорениями толкателя связаны пропорциональные им и массе толкателя силы инерции, учитывать которые приходиться при расчете замыкающих пружин, при определении напряжений в деталях механизма и т.д.), поэтому обычно в качества закона движения толкателя задаются кривой (или уравнением) относительных ускорений толкателя.

Технологические соображения в большинстве случаев заставляют обращаться к сложным законам движения.

В табл. 1...5 приведены некоторые законы движения толкателя, представленные в виде безразмерных коэффициентов относительных значений ускорений

и угла поворота Ку на фазе удаления. Коэффициент угла поворота Ку = j1р / jу меняется в пределах от 0 до I, а коэффициент ускорения в пределах

может изменяться по величине и по знаку. Для приведенных примеров вначале, а также в промежуточных положениях ускорение может изменяться скачком на конечную величину (мягкий удар за счет мгновенного изменения силы инерции). Для ряда законов ускорение меняется скачком в конце фазы удаления, в других случаях скачки на графиках ускорений могут отсутствовать.

Кинематические характеристики кулачкового механизма при задании функций через безразмерные коэффициенты могут быть представлены на фазе удаления в следующем виде:

перемещение толкателя -

кинематическая передаточная функция скорости толкателя -

;

кинематическая передаточная функция ускорения толкателя

.

3. Определение кинематических передаточных функций кулачкового механизма

Связь между кинематическими параметрами толкателя - ускорением

, скоростью

и перемещением

определяется известными соотношениями:

где Т - время одного оборота кулачка.

Так как закон изменения скорости кулачка неизвестен, приведенные зависимости нельзя использовать непосредственно, но их можно выразить через кинематические передаточные функции, которые не зависят от времени:

.

При расчете размеров и координат профиля кулачка кулачкового механизма определяющими являются ход толкателя, угол рабочего профиля кулачка и функциональная зависимость ускорения (относительного ускорения) толкателя от угла поворота кулачка. Если задать эту зависимость в аналитической форме, то последующим интегрированием могут быть получены зависимости кинематической передаточной функции скорости и перемещения толкателя.

Любую непрерывную дифференцируемую функцию вида

можно представить разложением в ряд:

, (1)

. (2)

(1) - полиномиальное разложение;

(2) - разложение в тригонометрический ряд;

- остаточный член.

Двойное интегрирование выражений (1) и (2) позволяет получить

, (3)

, (4)

, (5)

, (6)

где С1 , С2 - константы интегрирования.

Если предположить что

, то интегралы от Р из формул (3) ... (6) можно исключить. Таким образом, имея зависимости

вида (1) или (2), легко получить аналитические зависимости

вида (3) или (4) и зависимости

вида (5) или (6).

В программе QUL реализован алгоритм, вычисляющий значения первого и второго интеграла относительного ускорения толкателя для определения углов поворота кулачка. Следует заметить что

в общем виде может иметь точки разрыва.

При этом функция

при

разбивается на участки

,

где

- индекс участка (режима).

Так что функция

- кусочно-непрерывная дифференцируемая функция в области своего определения

, каждый

- й участок называется режимом, при этом

Чтобы избежать неопределенности в задании функции

, отрезки

открыты справа. Для обеспечения задания функции на

- ом режиме

предполагается, что

. Требование

не является обязательным.

Точность интегрирования определяется не шагом по углу поворота, а точностью задания функции на участке, т.е. величиной

.

Если исходная функция заданна в виде графика или таблицы значений, то решение получают при помощи численных или графических методов. Для определения передаточной функции скорости толкателя интегрируют заданную функцию ускорения толкателя, интегрируя полученную функцию скорости, находят функцию перемещения толкателя. Обычно применяется численное интегрирование методом трапеций по формулам:

где -

приращение угла поворота кулачка на шаге интегрирования,

N - число равноотстоящих точек, в которых заданны значения переменной.

Примечание:

В течение цикла движения толкатель кулачкового механизма должен переместиться из начального положения на величину хода h , а затем возвратиться в исходное положение, то есть перемещение толкателя на фазе удаления равно перемещению на фазе сближения. Следовательно, график кинематической передаточной функции скорости должен удовлетворять условию:

,

где jсо -угловая координата начальной точки фазы сближения.

Скорость и кинематическая передаточная функция скорости толкателя на фазах ближнего и дальнего выстоя равны нулю. Чтобы эти условия выполнялись необходимо выполнить соотношения

,

где jyp - угловое перемещение при разгоне на фазе удаления;

jср - угловое перемещение при разгоне на фазе сближения;

jст = jраб - (jсо + jср) - угловое перемещение при торможении на фазе сближения.

Эти условия необходимо учитывать при построении безразмерных графиков передаточной функции скорости и передаточной функции ускорения, выравнивая соответствующие указанным интегралам площади над осью абсцисс и под ней.

При работе над листом проекта с использованием графического интегрирования (рис. 3) все три графика располагают один под другим на одинаковой базе по оси абсцисс, которую удобно выбирать в пределах 150...240 мм. График скорости

толкателя (рис. 3б) получается (строится) методом графического интегрирования из графика ускорения толкателя. Для этого на продолжении оси t графика ускорений с левой стороны выбирается отрезок интегрирования К1 =30...50 мм. После построения графика скорости строится график перемещений толкателя рис. 3в. Для этого также на продолжении оси абсцисс t графика

откладывается отрезок интегрирования К2. Можно принимать К1 = К2. Или принять их равными mj. В зависимости от принятых отрезков интегрирования на графике

ордината

получается больше или меньше. Если частота вращения кулачка n1 (с-1) и максимальное перемещение (ход) толкателя h в исходных данных на проект заданы, то можно определить следующие масштабы:

Масштаб времени, мм / c

, (7)

Масштаб перемещений, мм / м

, (8)

Масштаб скорости, мм / мс-1

(9)

Масштаб ускорений, мм / мс-2

(10)

где

- максимальная ордината с графика перемещений точки В центра ролика толкателя, мм;

Рис.3

- угол рабочего профиля кулачка в градусах;

- база графика, мм;

- частота вращения кулачка, c-1.

Если в задании на проект значение угловой скорости или частоты вращения кулачка не заданы , то можно интегрировать заданный график по углу поворота кулачка

и получить графики кинематических передаточных функций. Для перехода от вычисленных интегралов

к действительным значениям кинематической передаточной функции скорости

и перемещения

определяются масштабы, которые вычисляются с учетом заданного максимального перемещения ( хода ) толкателя h и максимального вычисленного перемещения

из массива перемещений

.

Масштаб угла поворота, мм / рад

, (11)

Масштаб передаточной функции

скорости ,мм / м рад-1 ,

, (12)

Масштаб передаточной функции

ускорения, мм / м рад-2 ,

, (13)

где

- угол рабочего профиля кулачка в радианах,

К1 ,К2 - отрезки интегрирования, мм.

В массиве

отыскиваются максимальное

и минимальное

значения и соответствующие им углы

и перемещения толкателя

.

4. Определение основных размеров кулачкового механизма из условия ограничения угла давления

При выборе основных размеров кулачкового механизма - минимального радиуса кулачка

, смещения оси толкателя относительно оси вращения кулачка

или расстояния между осями вращения кулачка и толкателя

w, стремятся получить минимально возможные значения углов давления

, т.к. при этом уменьшаются реакции в кинематических парах, величина вращающего момента на валу кулачка, силы трения; повышается КПД и надежность механизма

Рис. 4

Углом давления называется угол между вектором силы, действующим на ведомое звено со стороны ведущего звена, и вектором скорости точки приложения этой силы. Связь угла давления с характером движения звеньев высшей кинематической пары и основными размерами механизма может быть установлена с использованием рис. 4 . Угол давления заключен между направлением вектора силы F, действующей со стороны кулачка на толкатель по нормали nn, проведенной в точке касания звеньев, и направлением вектора скорости точки В - VB , принадлежащей толкателю, перпендикулярного толкателю. Угол CO1D равен углу давления

, и

Из подобия треугольника плана скоростей и треугольника BO1D

После подстановки значений отрезков зависимость между углом давления и кинематическими параметрами механизма приобретет вид:

, (14)

где

- передаточная функция скорости точки В толкателя;

- расстояние между осями вращения кулачка и толкателя;

2 - длина толкателя;

- угол, определяющий положение толкателя относительно линии межосевого расстояния.

В случае, когда толкатель совершает прямолинейно-поступательное движение, выражение для определения угла давления имеет вид [2] :

, (15)

где

- смещение направляющей толкателя относительно оси вращения кулачка,

- координата точки В толкателя в системе координат, имеющих начало на оси вращения кулачка.

Величины

, входящие в формулу для определения

, являются переменными. Следовательно, угол давления также является переменной величиной и его текущие значения

i не должны превосходить определенный допустимый угол давления

Ji < [J].

Ранее было показано, что отрезок BD (рис. 4) изображает в масштабе mS передаточную функцию скорости точки В . Перпендикуляр к BD, проведенный через конец этого отрезка (точка D), составляет с прямой, проходящей через точку D и центр вращения кулачка О1, угол давления J. Следовательно, если известно положение оси вращения кулачка, не имея профиля кулачка, можно определить угол давления в различных точках i, построив для них отрезки, изображающие

, соответствующие положениям толкателя, определяемым перемещениями

(рис. 5 а, б) [1,2,5].

При проектировании механизма, когда положение оси вращения неизвестно, требуется выбрать его таким образом, чтобы любое из текущих значений Ji не превышало допустимых значений [J]. Для этого следует построить зависимость

и в каждой позиции

провести через конец отрезка кинематической передаточной функции скорости VqBi луч под углом [J] к вектору скорости в этой точке. Каждый луч удовлетворяет равенству J = [J] и ограничивает заштрихованную область допустимых решений (ОДР), в которой выполняется условие Ji

[J] для этого положения (рис. 5г). Центр вращения кулачка следует поместить в ОДР, общую для всех положений. Такое решение обеспечит выполнение условия Ji < [J] для полного цикла работы механизма.

Очевидно, что для механизма с поступательно перемещающимся толкателем, максимальные углы давления, как правило соответствуют характерным точкам фазового портрета

, в которых текущие значения кинематической передаточной функции скорости

принимают максимальные по абсолютной величине значения (рис. 5в).

В общем случае лучи, проведенные касательно к фазовому портрету под углом

, ограничивают ОДР, а точка пересечения лучей может быть выбрана центром вращения кулачка минимальных размеров.

Рис 5

Для механизма с качающимся толкателем целесообразно сделать аналогичные построения.

Такая геометрическая интерпретация ограничения по углу давления позволяет получить аналитические выражения для определения основных размеров механизма -

(или

w). Для этого нужно построить по вычисленным значениям функции перемещения толкателя

и передаточной функции скорости

кривую

: при поступательно движущемся толкателе в прямоугольной системе координат с началом в точке B0 на начальной окружности кулачка (рис 6б), при вращающемся толкателе - в полярной системе координат с началом в точке О2 на оси вращения толкателя (рис 6в). Текущие значения перемещения толкателя

откладываются по линии перемещения центра ролика (на рис. 6б - по оси

, на рис. 6в - по дуге радиуса

2), а текущие значения передаточной функции скорости

соответственно перпендикулярно оси

и - вдоль осевой линии толкателя. При построении принято [1,2], что передаточная функция скорости при удалении толкателя положительна, при сближении - отрицательна, т.е. вектор скорости точки В, будучи повернут на 90° в направлении вращения кулачка, совпадает с направлением отрезка кинематической передаточной функции скорости на фазовой плоскости.

Для механизма с качающимся толкателем перемещениям

(рис. 6а) соответствуют углы поворота толкателя (рис. 6в):

Из треугольника O2kn в котором известны длины двух сторон:

и угол между ними

, определяются расстояние между точками k и n по теореме косинусов и угол d:

Рис. 6

В треугольнике О1kn определяются углы и сторона О1k по теореме синусов:

;

Межосевое расстояние определяется из треугольника O1kO2 по теореме косинусов:

(16)

Угол между межосевой линией и ближним положением толкателя определяется из треугольника O1kO2 по теореме синусов:

(17)

Радиус начальной окружности кулачка определяется из треугольника O1B0O2 по теореме косинусов:

(18)

Расчетные соотношения для определения размеров кулачкового механизма с поступательно перемещающимся толкателем, получаемые с использованием рис. 6б имеют вид:

Смещение оси толкателя относительно оси вращения кулачка

(19)

Координата ближней точки толкателя

(20)

Радиус начальной окружности кулачка

(21)

При жестких ограничениях на габаритные размеры механизма принимают во внимание, что опасность заклинивания толкателя при силовом замыкании кинематической пары характерна только для фазы удаления, так как на фазе сближения толкатель движется под действием силы упругости пружины. Это позволяет расширить границы ОДР для положения оси вращения кулачка O1 с учетом допустимого угла давления, когда при работе механизма реверсивное движение кулачка не предусмотрено (кулачок вращается только по часовой стрелке либо только против). В таком случае на фазе сближения ограничение по углу давления не вводится или допустимый угол давления на фазе сближения принимается значительно большим, чем на фазе удаления.

На рис. 7 показано несколько ОДР для механизма с поступательно движущимся толкателем:

ОДР - направление вращения кулачка реверсивное, допустимые углы давления при удалении и сближении одинаковы;

Рис. 7

ОДР1 - направление вращения кулачка реверсивное, значения допустимых углов давления на фазе удаления и сближения различны;

ОДР2 - кулачок вращается только против часовой стрелки, предельное значение угла давления при сближении не регламентировано;

ОДР3 - кулачок вращается только по часовой стрелке, предельное значение угла давления при сближении не регламентировано;

ОДР4 - вращение кулачка реверсивное, смещение направляющей относительно оси вращения кулачка не допускается (

= 0).

Требования, предъявляемые к работе кулачкового механизма, определяют соответствующую ОДР, а следовательно, габаритные размеры,

(или

w), разные для каждого частного случая, и должны быть отражены при задании исходных данных для расчета на ЭВМ. Необходимо указать сведения о направлении вращения кулачка, допустимом угле давления и относительном расположении осей вращения кулачка и толкателя.

5. Определение координат профиля кулачка

Координаты точек профиля кулачка в программе для ЭВМ рассчитываются в полярной rO1y и декартовой ХO1Y системах координат. Начало координат совпадает с центром вращения кулачка, полярная ось или ось абсцисс проходит через начальную точку В0 на профиле кулачка.

Расчетные формулы для определения параметров кулачка с вращающимся толкателем получаются из схемы, изображенной на рис. 8. Полярные координаты - текущее значение радиуса центрового профиля кулачка

и угол

, определяющий его положение относительно оси:

(22)

, (23)

где

- межосевое расстояние;

2 - длина толкателя;

; (24)

- текущее значение угла поворота толкателя;

- текущее значение обобщенной координаты;

; (25)

. (26)

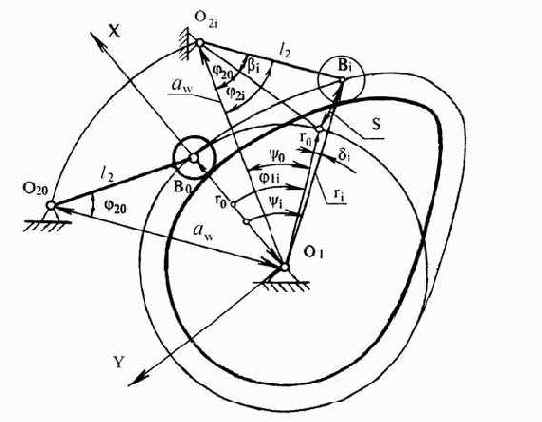
Рис.8

Координаты точки В профиля кулачка в декартовой системе

. (27)

Текущие значения углов давления

(28)

Координаты центрового профиля кулачка с поступательно перемещающимся толкателем определяются по формулам, выведенным по расчетной схеме, показанной на рис. 9.

Рис.9

Текущее значение радиуса центрового профиля

и угол

, определяющий его положение относительно полярной оси определяются по формулам :

(29)

, (30)

где

- координата ближней точки толкателя;

i - текущее значение перемещения очки В толкателя,

- внеосность толкателя

- текущее значение угла поворота кулачка;

. (31)

Наибольший радиус кулачка

(32)

где h - максимальное значение перемещения толкателя.

Координаты центрового профиля кулачка в декартовой системе координат

; (33)

. (34)

Текущие значения угла давления

                                              (35)

6. Описание программы расчета кулачкового механизма на ЭВМ

В соответствии с изложенной выше методикой составлена программа QUL для расчета размеров кулачкового механизма и координат профиля кулачка на ЭВМ Программа позволяет выполнять проектирование механизмов с вращающимся и поступательно перемещающимся толкателем при любом направлении вращения кулачка. Блок-схема программы показана на рис. 10.

Перечень исходных данных в порядке их ввода, обозначения и идентификаторы приводятся ниже:

1. Вариант задания на проект                                               -            ВАР

2. Ход толкателя, м                                                             h            Н

3. Угол рабочего профиля кулачка, град                            j1P          FIR

4. Число точек, задаваемых для описания графика

    передаточной функции ускорения толкателя                  -              N

5. Допустимый угол давления, град                                   [J]           UTD

6. Число точек разрыва передаточной функции

     ускорения толкателя                                                       -              NR

7. Длина коромыслового толкателя, м

2 L2

или внеосность толкателя , м

             Е

8. Идентификатор направления вращения кулачка              -            WR

9. Массив значений, описывающих график

    передаточной функции ускорения

             АQ

10. Массив, содержащий номера точек разрыва                -             NAQ

      и значения функции справа от точек разрыва

АQR

Если в исходных данных задана длина коромыслового толкателя, то рассчитываются межосевое расстояние, минимальный радиус и координаты центра вращения кулачка, координаты центрового профиля кулачка в декартовых и полярных координатах, углы давления.

Если в исходных данных не задана длина толкателя (

2= 0), то рассчитываются минимальный радиус кулачка, внеосность толкателя (если она не задана), координаты центрового профиля кулачка в декартовых и полярных координатах, углы давления для кулачкового механизма с поступательно перемещающимся толкателем.

Направление вращения кулачка задается идентификатором WR: при вращении по часовой стрелке WR=1, против - WR= -1, при реверсивном движении WR=0.

При вводе исходных данных заданный график ускорений должен быть достаточно точно описан массивом переменных

(AQ). Количество элементов N этого массива выбирается целым числом, кратным значению угла рабочего профиля кулачка

(FIR1), выраженного в градусах, а число элементов, описывающих функцию ускорения на фазах удаления, дальнего стояния и сближения - числами кратными значениям соответствующих углов

. Выполнение указанных рекомендаций позволяет разместить элементы массива ускорений точно на границах фаз рабочего профиля кулачка.

Если график функции ускорения имеет точки разрыва, то функция в этих точках должна быть описана особо: кроме значения функции слева от точки разрыва

(АQ(I)), входящего в массив

(АQ) должен быть указан номер значения функции в массиве

в точке разрыва - NАQ(j) и значение функции справа от точки разрыва -

(АQR(j)).

Значения функции ускорения справа от всех точек разрыва составляют массив

(АQR) размерностью NR (NR - число точек разрыва). Например, график ускорений, показанный на рис. 3a, описывается следующим образом:

АQ(i): 35.0; 30.0; 25,0; -12,5; -15.0; -17.5; -20,0; 0,0; -17,5; -15,0:

-12,5; -10,0; 30,0; 35,0.

NAQ(J), AQR(J): 2; -10,0; 6; 0,0; 7; -20,0: 11; 25,0.

В таблице результатов вначале печатаются исходные данные, характерные параметры фазового портрета

(FIK),

(FIN),

(VQK),

(VQN) и значения минимальных габаритов механизма

(R0),

(E) или

w (A). Затем для различных углов поворота кулачка

(FI1). выводятся на печать массивы значений

(АQ),

(VQ),

(S), координаты профиля кулачка в декартовых (

) и полярных (PSI, R) координатах и текущие значения углов давления J (TET). Распечатка таблицы результатов приведена в табл. 6.

7. Проектирование кулачковых механизмов графическим методом

Проектирование ведется в последовательности, которая указана в разделе 1.

1. Построение кинематических диаграмм методом графического интегрирования.

Построение начинают с заданного графика кинематической передаточной функции ускорения (рис. 3а, 11а). По оси абсцисс откладывают фазовые углы j1У + j1Д + j1С = jР

Масштаб по оси j вычисляют по формуле

м/рад ,

где j1P - угол рабочего профиля, град.,

b - база графиков, мм.

Максимальное значение ординаты графика на фазе удаления

задают произвольно, а максимальное значение ординаты на фазе сближения

вычисляют по условию равенства площадей из пропорции

.

Методом графического интегрирования строят график кинематической передаточной функции скорости толкателя. Для этого на продолжении оси j1 графика

выбирают произвольный отрезок интегрирования K1, делят ось абсцисс графика на интервалы, из середины каждого интервала восстанавливают перпендикуляр к оси j1 до пересечения с кривой

,

Таблица 6.

РЕЗУЛЬТАТЫ РАСЧЕТА КУЛАЧКОВОГО МЕХАНИЗМА С КАЧАЮЩИМСЯ ТОЛКАТЕЛЕМ

ВАРИАНТ А

ИСХОДНЫЕ ДАННЫЕ: Н=.020 FIR=130.0 WR=0 UTD=30.0 L2=.030

РЕЗУЛЬТАТЫ РАСЧЕТА: RO=.0533 A=.0716

FIK=30.0 VQK=.026 SK=.008

FIN=100 VQN=-.036 SN=.013

I	FI1	AQ	VQ	S
0	.0	15.000	.000	.000
1	10.0	13.000	.011	.000
2	20.0	10.000	.020	.004
3	30.0	3.000	.026	.008
4	40.0	-3.000	.026	.012
5	50.0	-10.000	.020	.016
6	60.0	-13.000	.011	.019
7	70.0	-15.000	.000	.020
8	80.0	.000	.000	.020
9	90.0	-25.000	-.022	.018
10	100.0	-10.000	-.036	.013
11	110.0	10.000	-.036	.007
12	120.0	25.000	-.022	.002
13	130.0	30.000	.000	.000

I	PSI	R	XB	YB	TET
0	0.	.0533	.0533	.0000	25.6664
1	10.4	.0542	.0533	-.0098	33.3188
2	21.4	.0568	.0529	-.0207	34.3708
3	32.3	.0607	.0513	-.0324	30.0000
4	42.6	.0652	.0480	-.0441	21.2215
5	52.3	.0692	.0423	-.0548	9.2179
6	61.9	.0719	.0338	-.0635	-3.6515
7	71.8	.0729	.0228	-.0692	-14.2965
8	81.8	.0729	.0104	-.0721	-14.2963
9	92.1	.0710	-.0026	-.0710	-27.0112
10	102.6	.0660	-.0144	-.0644	-30.0000
11	112.1	.0597	-.0225	-.0553	-23.0417
12	120.7	.0548	-.0280	-.0472	-1.8520
13	129.7	.0531	-.0340	-.0407	26.3327

средние значения ординат на каждом шаге проецируют на ось ординат и полученные точки соединяют с концом выбранного отрезка интегрирования.

Лучи, выходящие из точки конца отрезка интегрирования K1, характеризуются углами наклона, которые равны углам наклона касательных, проведенных в соответствующих точках к искомой интегральной кривой VqB(j1). Кривую VqB(j1) строят, проводя на каждом интервале отрезок, параллельный соответствующему лучу исходного графика

.Аналогично строят зависимость перемещения толкателя от угла поворота кулачка SB(j1) графическим интегрированием диаграммы VqB(j1), выбрав отрезок интегрирования K2.

Вычисляют масштабы по осям ординат построенных графиков

, используя известные соотношения (2,5...7) при графическом интегрировании.

2. Определение основных размеров кулачкового механизма.

Основные размеры механизма определяют с помощью фазового портрета, представляющего собой зависимость SB(VqB). Масштабы, выбранные по оси

(перемещений) и оси

должны быть одинаковыми. Для механизма с поступательно перемещающимся толкателем фазовый портрет строят в декартовой системе координат (рис. 11, б). с вращающимся толкателем - в полярной системе (рис. 12). По оси SB откладывают перемещения толкателя - в первом случае от начала координат в точке B0 вдоль линии перемещения толкателя , во втором - от точке В0 по дуге радиуса L2. проходящей через эту точку. Отрезки, соответствующие перемещениям толкателя откладывают, либо в масштабе mS графика перемещений, либо в масштабе

кинематической передаточной функции скорости.

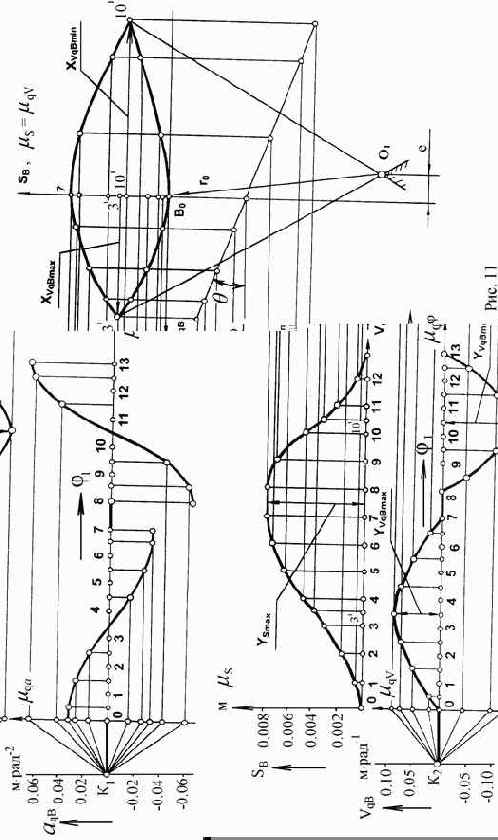
От полученных точек откладывают отрезки кинематических передаточных функций выбранном масштабе, соответственно перпендикулярно линии перемещения толкателя и вдоль толкателя.

Длины отрезков, изображающих кинематические передаточные функции скорости толкателя , вычисляют по формуле

мм,

Для определения направления вектора передаточной функции скорости следует вектор скорости толкателя повернуть на 90° в сторону вращения кулачка. При этом значение передаточной функции считается положительным при удалении толкателя и отрицательным при сближении.

Для удобства построения фазового портрета значения следует свести в таблицу 7.

Таблица 7

Номер позиции
Величина	1	2	3	...
YV, мм
m’s / mV×w1=KVq величина постоянная
XVq = KVqYV , мм

Фазовый портрет для механизма с поступательно движущимся толкателем можно построить и методом графического исключения параметра j1 из диаграмм SB(j1), VqB(j1). Для этого проводят вертикальную прямую - ось SB графика SB(VqB) (рис. 11б), продолжают ось j1 графика VqB(j1) до пересечения с осью SB, через полученную точку пересечения проводят прямую под углом q = arctg(mqv / ms) к горизонтали таким образом, чтобы при дальнейшем построении направление вектора передаточной функции соответствовало направлению вращения кулачка.

Фазовый портрет строят по точкам. Для выбранной позиции проводят через точку графика VqB(j1) горизонталь до пересечения с прямой, проведенной под углом q, и через полученную точку - вертикаль. Через точку графика SB(j1) в той же позиции проводят горизонтальную прямую до пересечения с построенной вертикалью. Точка пересечения - точка графика SB(VqB) в выбранной позиции. Аналогично получают все остальные точки графика, которые соединяют плавной кривой.

.

Рис.12

Если реверсивное движение кулачка не предусмотрено и значения углов давления на фазе сближения не заданы, достаточно построить только одну ветвь фазового портрета, соответствующую удалению толкателя.

Фазовый портрет для механизма с поступательно перемещающимся толкателем ограничивают в характерных точках лучами, которые проводят под заданными допустимыми углами давления к перпендикулярам, восстановленным в этих точках к векторам кинематических передаточных отношений.

На фазовом портрете механизма с качающимся толкателем лучи проводят в каждом положении. Внутри ограниченной лучами области допустимых решений выбирают положение оси вращения кулачка O1 и определяют искомые размеры кулачкового механизма

или

w .

3. Построение профиля кулачка.

При графическом построении профиля кулачка применяют метод обращения движения: всем звеньям механизма условно сообщают угловую скорость, равную - w1. При этом кулачок становится неподвижным, а остальные звенья вращаются с угловой скоростью, равной, но противоположной по направлению угловой скорости кулачка.

При построении профиля кулачка с внеосным поступательно движущимся толкателем (рис. 13), из центра O1 проводят окружности радиусами

и e в произвольном масштабе

. Касательно к окружности радиуса е проводят линию перемещения толкателя, располагая ее по отношению к центру вращения кулачка таким же образом, как на фазовом портрете и как задано в исходных данных (слева или справа). Точку пересечения линии перемещения толкателя с окружностью радиуса

- B0 соединяют с центром О1.

От полученного луча O1B0 в направлении w1 откладывают угол рабочего профиля кулачка j1P. Дугу, соответствующую углу j1P делят на части в соответствии с делением оси j1 на графике SB(j1). Через точки деления 1,2,3,... касательно к окружности радиуса е проводят лучи, являющиеся положениями толкателя в обращенном движении. От точек 1,2,3,... , лежащих на окружности радиуса

, вдоль проведенных лучей откладывают в масштабе

перемещения толкателя в каждой позиции. Соединяя полученные точки плавной кривой, получают теоретический (центровой) профиль кулачка.

Рис. 13

При построении профиля кулачка с качающимся толкателем (рис.14) из центра O1 проводят в масштабе ml окружности радиусами

w. Точку O1 соединяют с произвольно выбранной точкой O20 на окружности радиуса

w. От луча O1O20 в направлении -w1 откладывают угол рабочего профиля кулачка j1P.

Рис. 14

Дугу, соответствующую углу j1P делят на части в соответствии с делением оси j1 на графике SB(j1). Из точек O20,O21,O22,... проводят дуги радиусом

2 от точек 0,1,2,... на окружности радиуса

. От точек 0, 1, 2, ... по дугам откладывают в масштабе перемещения точки В толкателя - SB. Соединяя полученные точки В0 ...Вк плавной кривой, получают теоретический профиль кулачка. Из прочностных или геометрических соображений выбирают радиус ролика, учитывая соотношения

RP = (0,25-0,4) r0; или RP < 0,8 rmin,

где rmin - минимальный радиус кривизны центрового профиля кулачка.

Для получения конструктивного (рабочего) профиля кулачка строят эквидистантный профиль, отстоящий от центрового на величину радиуса ролика. Он получается как огибающая к дугам, проведенным из произвольных точек центрового профиля радиусом ролика (рис 15, 16).

Если технология изготовления кулачка предусматривает использование дуг окружностей, то найденный конструктивный профиль следует заменить профилем, составленным из дуг окружностей. Дуги окружностей должны соответствовать полученному профилю в пределах требуемой точности построений.

При такой замене следует помнить, что кулачок с профилем, составленным из дуг окружностей, всегда дает ступенчатый график ускорений, а график скорости всегда получается с изломом и только график перемещений может быть плавным.

Это следует учитывать при выборе числа заменяющих дуг окружностей.

Иногда в кулачковых механизмах по технологическим соображениям рабочая поверхность ведомого звена (толкателя) выполняется плоской. При вращательном движении кулачка использование плоских толкателей возможно лишь в тех случаях, когда радиус кривизны теоретического профиля не меняет своего знака, т.е. не имеет вогнутых участков [5].

Кроме плоских кулачковых механизмов, в практике машиностроения и приборостроения, используются и пространственные кулачковые механизмы. Примером пространственных кулачков могут служить кулачки барабанного типа, широко применяемые в автоматах. На поверхности кулачка, выполненного в виде цилиндра, конуса или гиперболоида вращения, имеется паз для ролика толкателя. В счетно-решающих устройствах употребляются пространственные кулачки-коноиды с двумя независимыми перемещениями [4]. Соответствующая рабочая поверхность такого коноида позволяет механически осуществлять требуемую зависимость угла поворота толкателя как функцию двух аргументов. Алгоритмы расчетов методы проектирования таких кулачковых механизмов приводятся в [2,3,5].

Таблица 1

Движение толкателя с мягкими ударами и постоянным ускорением

№ варианта и наименование	График ускорения на фазе удаления толкателя	Числовые значения коэффициента ¦²(К)
	графика		Ку	¦²(К) =
1 прямоугольный симметричный	n n 0.5 1 Ky 0 n	0 ... 5 0.5 ...	= 4 = - 4
2 прямоугольный несимметричный	n n Ky1 0.5 1 Ky 0 n	0 ... Ку1 Ку1 ... 1	= =
3 прямоугольный симметричный с нулевым участком	n n Ку1 0.5 Ку2 1 Ky 0 n	0 ... Ку1 Ку1.. 0.5 0.5 ... Ку2 Ку2.. 1	= 0 0
4 прямоугольный несимметричный с нулевым участком	n n Ку1 0.5 1 Ку 0 Ку2 n	0 ... Ку1 Ку1.. Ку2 Ку2.. 1	= 0

Таблица 2

Движение толкателя с мягкими ударами и косинусоидальным ускорением

№ варианта и наименование	График ускорения на фазе удаления толкателя	Числовые значения коэффициента ¦²(К)
графика		Ку	¦²(К) =
5 косинусоидаль-ный симметричный		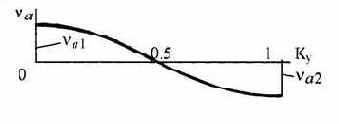0 0 ... 1	» 4.93 =
6 косинусоидаль- ный несимметричный		0 0...Ky1 Ку1 ... 1	= = =
7 косинусоидаль- ный с нулевым участком	n n Ку1 0.5 Ку2 1 Ky 0 n	0 0 ... Ку1 Ку1 ... Ку2 Ку2.. 1	= = p×nmax ¤ 2Ky1 = ×cospKy ¤ 2Ky 0

Таблица 3

Движение толкателя с мягкими ударами и равноубывающим ускорением

№ варианта и наименование	График ускорения на фазе удаления толкателя	Числовые значения коэффициента ¦²(К)
графика		Ку	¦²(К) =
8 равноубывающий симметричный	n n 0.5 1 Ky 0 n	0 0 ... 1 1	= 6 = 6(1-2Ку) = - 6
9 равноубывающий несимметричный	n n Ky1 0.5 1 Ky 0 n	0 0 ... Ку1 Ку1 Ку1 ... 1 1	= 3 / Ку1 = 3 / Ky1 - 3Ky / Ky12 0 = -3(Kу-Kу1) / (1-Kу1)2 = -3 / (1-Kу1)
10 прямоугольная трапеция	n n Ку1 0.5 Ку2 1 Ky 0 n	0 0 ... Ку1 Ку1.. 0.5 0.5 ... Ку2 Ку2.. 1	= 3 / (0.5+Kу1-Kу12) = ×(05-Kу) / (0.5-Kу1) ¾ « ¾
11 прямоугольник с косинусоидой	n n Ку1 0.5 Ку2 1 Ky 0 n	0 0 ... Ку1 Ку1 ... Ку2 Ку2 ... 1	= = ×sin

Таблица 4

Безударное движение толкателя с синусоидальным ускорением

№ варианта и наименование	График ускорения на фазе удаления толкателя	Числовые значения коэффициента ¦²(К)
графика		Ку	¦²(К) =
12 синусоидальный симметричный	n n 0.5 1 Ky 0 n	0 0.25 0 ... 1	0 = 2p =
13 синусоидальный несимметричный	n n Ку1 0.5 n 1 Ky 0	0.5 Ky1 0...Ky1 Ку1 ... 1 0	= p / Kу = = = -p / (1-Kу1)
14 синусоидальный с нулевым участком	n n Ку1 0.5 Ку2 1 Ky 0 n	0.5 Ky1 0 ... Ку1 Ку1 ... 0.5 0.5. 1	= = ×sin(pKу / Kу1) 0 аналогично

Таблица 5

Безударное движение толкателя со степенным законом ускорения

№ варианта и наименование	График ускорения на фазе удаления толкателя	Числовые значения коэффициента ¦²(К)
графика		Ку	¦²(К) =
15 степенной (3 - 4 - 5)	n n 0.5 1 Ky 0 n	0 ... 1	= 60(Ку-3Kу2+2Kу3) = 5.773
16 степенной (4 - 5 - 6 - 7)		0 ... 1	= 420×Ку2(1-4Ку+5Ку2-2Ку3) » 7.4
17 трапецеидальный	n n 0.5 1 Ку 0 Ку1 Ky2 C=0.5-0.5K1+(K2-K1)-2K1(K2-K1)-(K2-K1)2	0 ... К1 К1 ... К2 К2 ... 0.5	= 3 /С; = ×Kу / Kу1 = = ×

Начало

Ввод исходных данных

Вариант, Н, j1p , N, [J], NR, L2, WR

Ввод массивов: ускорений

,

точек разрыва NR,

Интегрирование графика ускорений

Определение параметров характерных точек

фазового портрета

Vqkmax, Vqnmax, jk, jn, Sk, Sn

Да Выбор Нет

схемы механизма

L2 = 0

         Расчет механизма                                     Расчет механизма

          с поступательно                                        с коромысловым

        перемещающимся                                            толкателем,

            толкателем,                                              идентификация WR

         идентификация WR

      Вычисление размеров                              Вычисление размеров

               g, d, ak, an,                                                  bk, bn, LVqk, LVqn,

           Lkn, Lo1k, e, S0, r0                                               d, dk, dn, g, Lkn

L01k,

, j20, r0

Вычисление координат

                           Вычисление координат

          профиля кулачка                                       профиля кулачка

         и углов давления                                        и углов давления

      bi, yi, ri, XBi, YBi, Ji                                         bi, y0, ri, j2i, di, yi ,

XBi, YBi, Ji

Печать исходных данных Печать исходных данных

и результатов расчета и результатов расчета

Останов Останов

Рис. 10