Геометрические параметры долбяков
Зуб долбяка имеет три режущие кромки: вершинную (периферийную), очерченную по дуге окружности, и две боковые, очерченные по эвольвенте или по кривой, близкой к эвольвенте (рис. 4.1). При проектировании долбяка передние и задние углы задаются по вершине. Для обеспечения лучших условий резания передний угол на вершине ga0 часто назначают положительным. В этом случае передняя поверхность будет являться конической поверхностью с осью, совпадающей с осью долбяка. При пересечении конической передней поверхности с винтовой эвольвентой задней поверхностью образуется боковая режущая кромка, проекция которой на торцевую плоскость нарезаемого колеса не будет эвольвентной. В результате обработанное зубчатое колесо будет также неэвольвентным вследствие чего будет иметь соответствующие погрешности. Размеры этих погрешностей зависят от принятых при конструировании долбяка величин передних и задних углов, поэтому они назначаются сравнительно небольшими.
 |
В свою очередь, передние и задние углы на боковых режущих кромках (gб0,
aб0) зависят от принятых переднего и заднего углов на вершине (ga0, и aa0). Расчетным задним углом на боковой режущей кромке является задний угол в сечении по делительному цилиндру. Для его получения рассечем зуб долбяка по делительному цилиндру. Линии пересечения боковых задних поверхностей зубьев с цилиндром будут представлять собой винтовые линии, так как боковые поверхности являются эвольвентными винтовыми поверхностями. Угол наклона этих винтовых линий и является задним углом в сечении по делительному цилиндру. Полученное сечение развернем на плоскость (рис. 4.2). Тогда винтовые линии превратятся в прямые, наклоненные к вертикали под углом aб0, который определяется следующим образом:

где А – величина положительного исходного расстояния; S0P – толщина зуба долбяка по делительной окружности в сечении по передней поверхности; S0 – толщина зуба долбяка по делительной окружности в исходном сечении.

Рис.4.2 Определение бокового заднего угла долбяка в сечении по делительному цилиндру
Принимая во внимание равенство

и подставляя выражение для S0P в формулу (4.1), после выполнения ряда сокращений, получим

С точки зрения протекания процесса резания целесообразно знать задние углы на боковых режущих кромках в сечении, нормальном к кромке, так как именно эти углы определяют величину износа по задней поверхности. Для эвольвентной режущей кромки таким сечением будет сечение плоскостью, касательной к основному цилиндру и проходящей через рассматриваемую точку режущей кромки.
На рис. 4.3 показан зуб долбяка со стороны передней поверхности, сечение зуба плоскостью N–N, нормальной к боковой режущей кромке и развернутое на плоскость сечение зуба основным цилиндром. Рассматривая прямоугольные треугольники




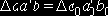

где aбN0 - величина действительного (измеренного в плоскости, нормальной к режущей кромке) заднего угла на боковых сторонах зуба долбяка; ab0 - величина заднего угла на поверхности основного цилиндра долбяка.
Задний угол на боковой режущей кромке на поверхность основного цилиндра определяется как угол наклона винтовой линии, образуемой при пересечении поверхности основного цилиндра с боковой задней поверхностью, являющейся винтовой эвольвентной поверхностью. Вследствие этого выполняется следующее равенство:

где


(в приведенной формуле d0 – делительный диаметр долбяка) и проведя элементарные преобразования, получим:

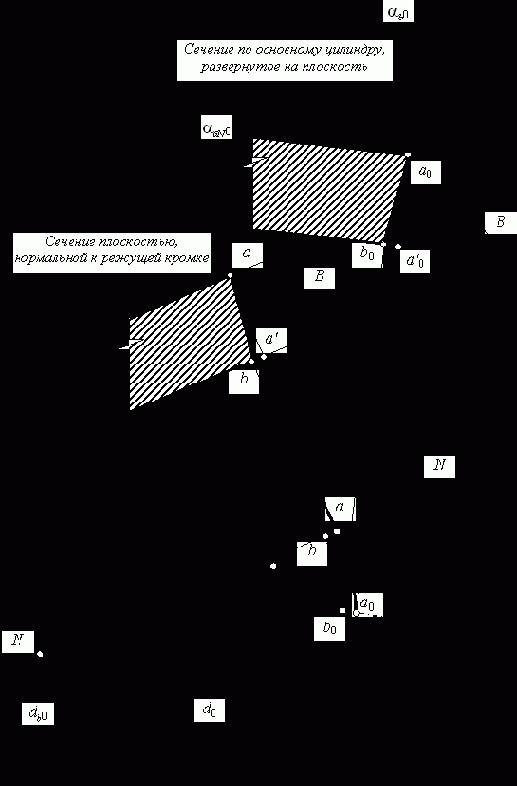
Рис.4.3 Определение бокового заднего угла в сечении, нормальном к режущей кромке
Шаг винтовой эвольвентной поверхности, частью которой является боковая задняя поверхность зуба долбяка, является постоянным, поэтому шаги винтовых линий, которые образуются при пересечении боковой поверхности делительным и основным цилиндром, одинаковы.
На основании этого:

где aб0 - боковой задний угол на делительном цилиндре. Подставив полученное выражение в формулу (4.7), получим:

Приняв во внимание формулу (4.3) и произведя необходимые преобразования, получим:

Учитывая доказанное ранее равенство углов aбN0 и ab0, получим формулу для определения бокового заднего угла в сечении, нормальном к режущей кромке:

Так как для любого долбяка задний угол при вершине и угол профиля зубьев являются постоянными величинами, полученная формула показывает, что задний угол на боковой режущей кромке в нормальном сечении не изменяется вдоль всей режущей кромки и является постоянной величиной.
Так как передняя поверхность долбяка является конической, очевидно, что передний угол на боковых режущих кромках в радиальных сечениях для всех точек зуба долбяка одинаков и равен переднему углу при вершине зубьев ga0. Однако закономерности протекания процесса резания в значительно большей степени определяются величинами передних углов в сечениях, нормальных к режущей кромке (в каждой из рассматриваемых точек). В секущей плоскости N-N, нормальной к режущей кромке долбяка, передний угол gбN0 измеряется между касательной к передней поверхности долбяка в рассматриваемой точке А и плоскостью, перпендикулярной к оси долбяка (рис. 4.4). Применительно к долбяку нормаль к профилю в точке А совпадает с образующей АВ, касательной к основной окружности. В сечении АВ, расположенном по отношении к АО0 (О0-центр обрабатываемого колеса) под углом (90°-aА), передний угол gбN0 определяется по формуле


где aА – угол давления эвольвенты для рассматриваемой точки A. Угол давления эвольвенты в рассматриваемой точке А определяется по формуле

где rb0 - радиус основной окружности долбяка; rA ? радиус цилиндра, на котором лежит рассматриваемая точка режущей кромки.Так как угол давления эвольвенты профиля по высоте зуба изменяется от 0° (для точки, лежащей на основной окружности) до величины, близкой к 30° (для точки, лежащей на окружности вершин зубьев), изменяется и боковой передний угол. Как правило, боковой передний угол по высоте профиля зуба долбяка изменяется от 0° до 2°?4°.
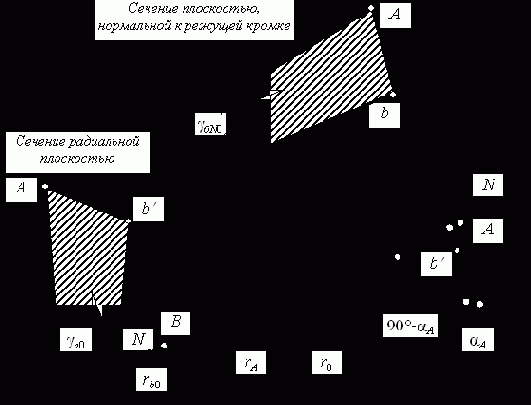
Рис.4.4 Схема к определению бокового переднего угла в сечении, нормальном к режущей кромке
Литература
1. ГОСТ 13755-81. Передачи зубчатые цилиндрические эвольвентные. Исходный контур. - М., 1981. - 5 с.
2. ГОСТ 1643-81. Передачи зубчатые цилиндрические. Допуски. - М., 1981. - 69 с.
3. ГОСТ 25751-83. Инструменты режущие. Термины и определения общих понятий. - М., 1983. - 25 с.
4. ГОСТ 7.1-84. Библиографическое описание документа. Обшие требования и правила составления. - М., 1983. - 25 с.
5. Долбяки зуборезные чистовые прямозубые. Методики расчета. РТМ АГВ 85.24?75, РТМ АГВ 85.25?75. - Волгоград, 1975.
6. Иноземцев Г.Г. Проектирование металлорежущих инструментов: Учеб. пособие для втузов по специальности «Технология машиностроения, металлорежущие станки и инструменты» - М.: Машиностроение,1984. - 270 с.
7. Металлорежущие инструменты: Учебник для вузов по специальностям «Технология машиностроения», «Металлорежущие станки и инструменты» /Г.Н.Сахаров, О.Б.Арбузов, Ю.Л.Боровой и др. - М.: Машиностроение, 1989. - 328 с.
8. Мойсеенко О.И., Павлов Л.Е., Диденко С.И. Твердосплавные металлорежущие инструменты. - М.: Машиностроение, 1977. - 190 с.
9. Нарожных А.Т., Скребнев Г.Г., Соколов Д.В. Проектирование протяжек: Учебное пособие / ВолгГТУ, Волгоград, 1995. - 85 с.
10. Нарожных А.Т., Скребнев Г.Г., Токарев В.В. Проектирование фасонных резцов: Учебное пособие / ВолгГТУ, Волгоград, 1999. - 88 с.
11. Основы проектирования режущих инструментов с применением ЭВМ / П.И.Ящерицын, Б.И.Синицын, Н.И.Жигалко и др. - Минск: Вышэйшая школа,1979. - 304 с.
12. Передачи зубчатые. ГОСТ 16530-83, ГОСТ 16531-83, ГОСТ 16532?70. - М., 1987. - 119 с.
13. Правила выполнения чертежей различных изделий. ГОСТ 2.402-68, ГОСТ 2.403-75, ГОСТ 2.405-75, ГОСТ 2.406-76, ГОСТ 2.407-75, ГОСТ 2.408-68, ГОСТ 2.409-74, ГОСТ 2.421-75, ГОСТ 2.422-70, ГОСТ 2.425-74, ГОСТ 2.426-74. - М., 1978. - 72 с.
14. Правила оформления рукописи (авторский текстовый оригинал): Методические указания / Сост.
Л.П.Кузнецова, В.Н.Подлеснов, Е.Н.Андросюк; Под. ред. проф. Ю.В.Попова; ВолгГТУ. - Волгоград, 1995. - 44 с.
15. Правила оформления графической части и пояснительной записки дипломных и курсовых проектов: Методические указания / Сост. И.Г.Ткаченко, Г.Г.Скребнев; ВолгГТУ. - Волгоград, 1995. - 30 с.
16. Проектирование и расчет металлорежущего инструмента на ЭВМ: Учебное пособие для втузов / О.В.Таратынов, Г.Г.Земсков, Ю.П.Тарамыкин и др. - М: Высшая школа, 1991. - 423 с.
17. Производство зубчатых колес: Справочник / С.Н.Калашников, А.С.Калашников, Г.И.Коган и др.; Под общей редакцией Б.А.Тайца. - М: Машиностроение, 1990. - 464 с.
18. Романов В.Ф. Расчеты зуборезных инструментов. - М.: Машиностроение, 1969. - 251 с.
19. Семенченко И.И., Матюшин В.М., Сахаров Г.Н. Проектирование металлорежущих инструментов. - М.: Государственное научно-техническое издательство машиностроительной литературы, 1963. - 952 с.
20. Семенченко И.И. Режущий инструмент. Проектирование и производство. Т.3. - М., Свердловск: Государственное научно-техническое издательство машиностроительной литературы, 1944. - 559 с.
21. Справочник инструментальщика / И.А.Ординарцев, Г.В.Филиппов, А.Н.Шевченко и др. - Л.: Машиностроение, 1987. - 846 с.
22. Справочник конструктора-инструментальщика: Под общей редакцией В.И.Баранчикова- М.: Машиностроение, 1994. - 560 с.
23. Червячные зуборезные фрезы: Учебное пособие / Токарев В.В., Скребнев Г.Г., Нарожных А.Т. и др. /
ВолгГТУ, Волгоград, 1988. - 136 с.
[1]
Напомним, что при обработке зубчатого колеса червячной зуборезной фрезой или зуборезной гребенкой, центроидой зубчатого колеса является окружность, а центроидой инструмента (инструментальной рейки) - прямая [23, с.6].
[2]
Следует отметить, что в ряде случаев из твердого сплава выполняются и цельные долбяки малых модулей (m=1,5?3 мм). Изготавливаются только насадные цельные твердосплавные долбяки.
[3] Для того, чтобы сохранить общепринятую нотацию, угол давления на вершине зуба долбяка следовало бы обозначать aа0. Однако при проектировании долбяков этим символом обозначается задний угол на вершинной режущей кромке инструмента. Для того, чтобы избежать противоречий, в данном пособии угол давления на вершине зуба обозначен символом zа0.
Методика проектирования прямозубых долбяков
После расчета дополнительных параметров зубчатой передачи производится собственно проектирование долбяка, то есть расчет конструктивных и геометрических параметров, определяющих долбяк как геометрическое тело (рис.5.2). В дальнейшем изложении будем полагать, что долбяк проектируется для обработки большего колеса зубчатой передачи (колеса с числом зубьев z2). В случае, если долбяк проектируется для обработки шестерни (меньшего колеса с числом зубьев z1), в последующих формулах следует заменить индекс при переменных «2» на индекс «1». В остальном методика расчета остается неизменной. Полный перечень исходных данных, необходимых для проектирования зуборезного долбяка, представлен в табл. 6.3.

Рис.6.4 Принципиальная схема проектного расчета дискового долбяка
Исходные данные для проектирования дискового зуборезного долбяка
| Обозначение параметра | Наименование параметра | Примечания |
| Параметры зубчатой передачи, задаваемые чертежом изделия | ||
| m | Модуль зубчатой передачи, мм | |
| x2 | Коэффициент смещения для обрабатываемого колеса | |
| a | Угол профиля исходного контура | |
| ha* | Коэффициент высоты головки зуба обрабатываемого колеса | |
| hf* | Коэффициент высоты ножки зуба обрабатываемого колеса | Коэффициент высоты ножки зуба может быть определен через коэффициент граничной высоты: hf*=hl*-ha* |
| b | Угол наклона зубьев обрабатываемого колеса | Угол наклона зубьев долбяка на делительном цилиндре b0 принимается равным углу наклона зубьев колеса b |
| Параметры зубчатой передачи, определяемые расчетом | ||
| Dy | Коэффициент уравнительного смещения передачи | Определяется по формуле (6.15), см. С.37 |
| d2 | Делительный диаметр обрабатываемого колеса, мм | Определяется по формуле (6.11), см. С.36 |
| da2 | Диаметр окружности вершин зубьев обрабатываемого колеса, мм | Определяется по формуле (6.16), см. С.37 |
| df2 | Диаметр окружности впадин обрабатываемого колеса, мм | Определяется по формуле (6.17), см. С.37 |
| db2 | Диаметр основной окружности обрабатываемого колеса, мм | Определяется по формуле (6.18), см. С.37 |
| rp2 | Радиус кривизны в точке начала активной части профиля зуба обрабатываемого колеса, мм | Определяется по формуле (6.20), см. С.38 |
| Дополнительные параметры | ||
| с0* | Коэффициент радиального зазора в передаче долбяк?колесо | В большинстве случаев расчета может быть принято с0*=0,25 |
| j | Боковой зазор в зацеплении, мм | Величина бокового зазора выбирается в зависимости от степени точности передачи по нормам плавности работы. Методика определения величины бокового зазора подробно изложена в [23, с.48-51]. |
| Степень точности зубчатой передачи | ||
| Модель зубодолбежного станка, на котором будет производиться обработка колес | ||
| Модель станка, на котором будет производиться шлифование профиля зубьев долбяка |
1. Первым шагом в проектном расчете долбяка является определение номинального делительного диаметра и числа зубьев инструмента. При выборе делительного диаметра и числа зубьев принимаются в расчет следующие соображения:
а) возможность использования долбяка с выбранным номинальным делительным диаметром на имеющихся моделях зубодолбежных станков. Обычно стремятся на станке заданной модели применять долбяки одного номинального делительного диаметра. Данные о параметрах различных моделей зубодолбежных станков [17, с.93?94] представлены в табл. 6.5;
б) рекомендации ГОСТ 9323–79 в отношении выбора номинального делительного диаметра долбяка. Параметры стандартных долбяков ГОСТ 9323–79 приведены в табл. 5.2 и 5.3 (см. С.27). В табл. 6.4 приведены данные о рекомендованных значениях номинальных делительных диаметров долбяков. При проведении проектного расчета, ориентировочное число зубьев долбяка определяется по формуле

где d0ном – номинальный делительный диаметр долбяка согласно ГОСТ 9323–79, мм. Полученное значение числа зубьев долбяка округляется до целого, желательно четного числа. Целесообразно принимать число зубьев долбяка в интервале от 22 до 40. Такое число зубьев позволяет нарезать зубчатые колеса во всем диапазоне зубьев, обеспечивая практически приемлемые геометрические параметры переходных кривых. Однако, на практике, для долбяков больших модулей, а также для нарезания колес внутреннего зацепления в ряде случаев приходится принимать число зубьев меньше 22. Кроме того, в целях расширения диапазона модулей, охватываемых данным номинальным диаметром, а также для повышения стойкости долбяков проектируются долбяки с числом зубьев больше 40;
в) возможность обработки долбяка на имеющихся моделях зубошлифовальных станков. При изготовлении зубья долбяков шлифуются на зубошлифовальных станках. Поэтому при проектировании долбяка число его зубьев необходимо выбрать таким, чтобы оно было равно или кратно числу зубьев одного из делительных дисков, которые в виде набора прилагаются к зубошлифовальным станкам.
Параметры стандартного набора эвольвентных копиров и делительных дисков к зубошлифовальным станкам приведены в табл. 6.4.
Таблица 6.4
Ряды значений параметров, рекомендованные к использованию при проектировании долбяков
|
Наименование параметра |
Обозначение параметра |
Рекомендованный ряд значений |
|
Номинальный диаметр долбяка, мм |
d0ном |
25; 38; 50; 80; 100; 125; 160; 200 |
|
Число зубьев делительных дисков, прилагаемых к зубодолбежным станкам |
zдиск |
17; 18; 20; 21; 22; 23; 24; 2\5; 27; 28; 29; 30; 31; 32; 34; 36; 37; 38; 40; 41; 42; 43; 44; 45; 46; 47; 48; 51; 52; 53; 54; 58; 60; 61; 62; 63; 64; 66; 67; 68; 70; 72; 73; 74; 75; 76; 78; 80; 83; 88; 90; 100; 102; 103; 115 |
|
Диаметры основных окружностей эвольвентных копиров |
dbK |
8; 12; 15; 25,4; 26; 34.4; 38.1; 39.4; 45.2; 50; 50.8; 55; 62; 63.5; 70.8; 72; 73,4; 75; 76.2; 88.9; 99; 99.6; 100; 101.6; 103; 107; 125; 142; 150; 162; 164; 171; 178; 180; 198; 202; 225 |
Основные параметры зубодолбежных станков
|
Завод-изготовитель |
Корсунь-Шевченковский станкостроительный завод (Украина) |
Егорьевский станкостроительный завод (Россия) |
|||
|
Модель станка |
5111 |
5А122 |
5А122Ф4 |
5А140П |
5А130* |
|
Наибольший диаметр заготовки |
80 |
250 |
200 |
500 |
250 |
|
Наибольший модуль нарезаемого колеса |
1 |
6 |
5 |
8 |
10 |
|
Наибольшая ширина венца |
20 |
50 |
50 |
100 |
105 |
|
Наибольший делительный диаметр долбяка |
40 |
100 |
100 |
100 |
|
|
Частота движения долбяка (двойных ходов в мин.) |
26?1600 |
195-1200 |
125-1250 |
55-560 |
40-100 |
|
Мощность главного привода, кВт |
1,1 |
3 |
11 |
5/6,3/10 |
22 |
|
Масса станка, т |
1,5 |
5 |
5,4 |
7,5 |
16 |
|
Завод-изготовитель |
Клинский станкостроительный завод (Россия) |
||||
|
Модель станка |
5М150П |
5М161 |
51А80ПФ2 |
51А125ПФ2 |
51А200ПФ2 |
|
Наибольший диаметр заготовки |
800 |
1250 |
800 |
1250 |
2240 |
|
Наибольший модуль нарезаемого колеса |
12 |
12 |
12 |
12 |
12 |
|
Наибольшая ширина венца |
160 |
170 |
190 |
190 |
200 |
|
Наибольший делительный диаметр долбяка |
200 |
200 |
200 |
200 |
200 |
|
Частота движения долбяка (двойных ходов в мин.) |
33-188 |
33-212 |
30-327 |
30-327 |
5-400 |
|
Мощность главного привода, кВт |
4,8/5,7/7,5 |
4,8/5,7/7,5 |
10/6,3/5 |
10/6,3/5 |
10 |
|
Масса станка, т |
9,5 |
10,5 |
11,5 |
11,7 |
18,4 |
|
Фирма -изготовитель |
Либхер (ФРГ) |
Сейкс (Англия) |
|||
|
Модель станка |
WS201 |
WS401 |
WS501 |
V1250 |
V400 |
|
Наибольший диаметр заготовки |
250 |
400 |
500 |
250 |
400 |
|
Наибольший модуль нарезаемого колеса |
6 |
8 |
8 |
6 |
6 |
|
Наибольшая ширина венца |
50 |
80 |
140 |
130 |
130 |
|
Наибольший делительный диаметр долбяка |
186 |
200 |
200 |
100 |
100 |
|
Частота движения долбяка (двойных ходов в мин.) |
320-2060 |
200-1800 |
31-500 |
50-1000 |
50-1000 |
|
Масса станка, т |
6 |
7,6 |
8,3 |
3,9 |
|
Фирма-изготовитель |
Лоренц (ФРГ) |
||||
|
Модель станка |
SN4 |
SN5 |
SN8 |
SN10 |
LS150 |
|
Наибольший диаметр заготовки |
210 |
500 |
630 |
1000 |
150 |
|
Наибольший модуль нарезаемого колеса |
4 |
5 |
8 |
10 |
5 |
|
Наибольшая ширина венца |
60 |
75 |
180 |
180 |
42 |
|
Наибольший делительный диаметр долбяка |
100 |
125 |
125 |
200 |
125 |
|
Частота движения долбяка (двойных ходов в мин.) |
236-900 |
30-424 |
47-300 |
21-175 |
265-1250 |
|
Масса станка, т |
3,6 |
4,1 |
5,5 |
6 |
5,7 |
2. После выбора числа зубьев долбяка производится определение фактического делительного диаметра долбяка, который рассчитывается по формуле
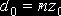
где z0 – фактическое число зубьев долбяка, выбранное с учетом номинального делительного диаметра и числа зубьев делительного диска зубошлифовального станка.
3. Производится определение теоретического диаметра основной окружности долбяка:

4. Производится определение угла установки салазок зубошлифовального станка. Для равномерного износа шлифовального круга, повышения точности профиля долбяка, достижения большей универсальности в использовании зубошлифовальных станков при шлифовании зубьев долбяка салазки зубошлифовального станка устанавливаются под некоторым углом к оси шлифовального круга, который обозначается aуст. При этом необходимо выдержать условия:


Учитывая сказанное выше, для определения угла установки салазок зубошлифовального станка выполняются следующие действия:
а) определяется диаметр основной окружности эвольвентного копира при условии шлифования зубьев долбяка с углом установки салазок зубошлифовального станка


б) определяется диаметр основной окружности эвольвентного копира при условии шлифования зубьев долбяка с углом установки салазок зубошлифовального станка


в) фактический диаметр основной окружности эвольвентного копира dbК должен находиться в интервале от d¢bK до d²bK и выбирается из ряда диаметров эвольвентных копиров, представленных в табл. 6.4.
г) определяется угол установки салазок зубошлифовального станка:

где dbK – фактический диаметр основной окружности копира зубошлифовального станка. Расчет ведется с точностью до 0,000001, а полученный результат округляется до 1¢ (0,01°).
5. На следующем шаге расчета осуществляется выбор углов резания на вершине зуба долбяка. Как уже отмечалось, наличие положительных передних и задних углов на вершине зуба долбяка ведет к появлению погрешностей нарезаемого колеса. Размеры этих погрешностей зависят от принятых величин передних и задних углов (чем больше эти углы, тем больше погрешности). Поэтому передние и задние углы долбяков выбираются сравнительно небольшими.
Передний угол ga0 для чистовых долбяков принимается равным 5°, а для обдирочных долбяков ga0=10°.
Задний угол на вершине назначается в зависимости от угла главного профиля зуба нарезаемого колеса. Рекомендованные величины заднего угла aа0 приведены в табл. 6.6.
Таблица 6.6
Величина заднего угла на вершине зуба долбяка
|
Угол главного профиля нарезаемого колеса, a |
Задний угол на вершине долбяка aа0 |
|
15?17° |
7°30’ |
|
18?25° |
6° |
|
26?30° |
4° |
Вследствие совместного влияния на профиль инструмента переднего и заднего углов, профильный угол долбяка будет отличаться от угла профиля нарезаемого колеса:

Расчет ведется с точностью до 0,000001, а полученная величина a0K округляется до 1І (0,0001°).
7. Производится определение расчетных геометрических параметров долбяка на боковых режущих кромках.
а) боковой задний угол в нормальном сечении к боковой режущей кромке определяется по формуле

На угол aбN0 поворачивается шлифовальная головка станка при изготовлении долбяка. Значение aбN0 вносится в рабочий чертеж инструмента. Расчет ведется с точностью до 0,000001, а полученная величина aбN0 округляется до 1І (0,0001°);
б) боковой задний угол на поверхности делительного цилиндра определяется по формуле

Расчет ведется с точностью до 0,000001, а полученная величина aб0 округляется до 1І (0,0001°).
в) передний угол в нормальном сечении к боковой режущей кромке в точке, лежащей на делительном цилиндре определяется по формуле

Расчет ведется с точностью до 0,000001, а полученная величина округляется до 1І (0,0001°).
8. Определение фактического диаметра основной окружности долбяка производится по формуле

9. Определяются размеры долбяка в исходном сечении. Известно, что в исходном сечении долбяк представляет собой зубчатое колесо без смещения, и размеры его точно соответствуют размерам нарезаемого колеса. Поэтому при определении размеров долбяка в исходном сечении используются те же формулы, которые применяются при определении параметров зубчатого колеса, сопряженного в передаче с тем колесом, которое обрабатывается долбяком:
а) толщина зуба долбяка по дуге делительной окружности определяется по формуле

где толщина зуба обрабатываемого колеса по дуге делительной окружности S2 с учетом бокового зазора в передаче определяется по формуле

б) высота головки зуба долбяка принимается равной высоте ножки зуба обрабатываемого колеса:
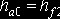
где высота ножки зуба колеса hf2 рассчитывается по формуле

в) высота ножки зуба долбяка определяется по формуле
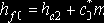
где высота головки зуба обрабатываемого колеса ha2 определяется по формуле

Расчет ведется с точностью до 0,0001, а полученные величины S0, hf0 и ha0 округляются до 0,001;
г) диаметр окружности вершин зубьев долбяка в исходной плоскости определяется по формуле

д) угол давления на вершине зуба долбяка[3] определяется по формуле

е) толщина зуба долбяка на окружности вершин определяется по формуле

10. На шаге 10 производится определение положительного исходного расстояния. Теоретические аспекты определения положительного исходного расстояния изложены в разделе 2 (см. С.11). Положительное исходное расстояние определяется по следующей методике:
а) рассчитывается величина положительного исходного расстояния, при котором гарантируется обработка полной высоты активной части профилей зубьев колеса. В первую очередь определяется станочный угол зацепления нового (индекс «Н») долбяка, обеспечивающий полную обработку рабочей части профиля зуба колеса по формуле

Расчет ведется с точностью до 0,000001, а полученная величина a¢wН округляется до 1І (0,0001°).
Положительное исходное расстояние, обеспечивающее полную обработку рабочей части профиля зуба колеса рассчитывается по формуле

б) положительное исходное расстояние, лимитируемое заострением зубьев долбяка, определяется по формуле

где Sa0min – минимально допустимая длина периферийной (вершинной) режущей кромки.
Минимальная длина периферийной режущей кромки определяется по формуле

в) из двух полученных значений a¢Н и a²Н для дальнейших расчетов принимают меньшее, которое обозначают символом aН.
11. Производится определение отрицательного исходного расстояния. Как указывалось выше (см. раздел 2, с.11), отрицательным исходным расстоянием называется расстояние от исходного сечения до торцевого сечения предельно сточенного долбяка. При проектировании долбяка определяется максимальная величина отрицательного исходного расстояния, при которой обеспечивается выполнение трех условий: условия отсутствия срезания головки зуба колеса; условие полной обработки зубьев, условие отсутствия подрезания ножки зуба колеса:
а) производится определение отрицательного исходного расстояния, при котором гарантируется отсутствие среза на головках зубьев колес или неполной обработки головок зубьев. Для этого определяется станочный угол зацепления предельно сточенного долбяка, гарантирующий отсутствие среза на головках зубьев колес или неполной обработки головок зубьев по формуле

где r2max - наибольший радиус кривизны профиля зуба нарезаемого колеса:

r0 ? минимальный радиус кривизны профиля зуба долбяка. Величина минимального радиуса кривизны профиля зуба долбяка определяется в зависимости от номинального диаметра d0:
d0 r0
Менее 75 мм.......................... 2 мм
75?99 мм........................... 3 мм
100 мм и более........................ 5 мм
Расчет ведется с точностью до 0,000001, а полученная величина a¢wC округляется до 1І (0,0001°).
Отрицательное исходное расстояние, при котором отсутствует срез на головках зубьев колес или неполная обработка головок зубьев выполняются по формуле

б) определение отрицательного исходного расстояния из условия отсутствия подрезания ножки зуба нарезаемого колеса производится только в том случае, когда диаметр окружности впадин обрабатываемого колеса меньше диаметра основной окружности этого колеса, то есть имеет место неравенство

При этом определяется станочный угол зацепления, при котором происходит начало подрезания ножки зуба обрабатываемого колеса по формуле

Расчет ведется с точностью до 0,000001, а полученная величина a²wC округляется до 1І (0,0001°).
Отрицательное исходное расстояние предельно сточенного долбяка, при котором будет происходить начало подрезания ножек зубьев нарезаемых колес, определяются по формуле

в) из двух полученных значений a¢C и a²C для дальнейших вычислений выбирается одно, которое обозначается aC. Величины a¢C и a²C могут иметь разные знаки или обе быть отрицательными. В случае наличия разных знаков за расчетные значения AC следует принять положительную величину и плоскость окончательной переточки долбяка расположить правее исходного сечения I?I (рис. 6.5, б). При отрицательных значениях a¢C и a²C за расчетную величину необходимо принять меньшее по абсолютной величине и плоскость окончательной переточки долбяка расположить левее исходного сечения I?I (рис. 6.5, а).

а б
Рис.6.5 Схема к определению расчетных значений исходных расстояний
12. Производится определение высоты долбяка. Высота долбяка определяется как сумма высоты рабочей части долбяка и высоты окончательно сточенного долбяка (рис. 6.5).

где BP – высота рабочей части долбяка; BС – высота окончательно сточенного долбяка. Высота окончательно сточенного долбяка берется из табл. 6.7. Высота рабочей части долбяка чаще всего определяется расчетными значениями исходных расстояний.
Так, по рис. 6.5, а высота рабочей части
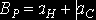
а по рис. 6.5, б

Однако, помимо исходных расстояний, высота долбяка может лимитироваться технологическими требованиями шлифования профиля зубьев долбяка. При шлифовании зубьев долбяка отсутствует продольная подача круга относительно долбяка. В результате этого впадина зуба получается вогнутой, что может привести к ослаблению или подрезу зубьев долбяка (рис. 6.6). Эти ограничения не относятся к категории расчетных и задаются в виде таблицы максимальных высот долбяка, составленной на основе практического опыта. Рекомендуемые высоты рабочей части долбяка, допустимые технологическими требованиями, приведены в табл. 6.7.
Таблица 6.7
Рекомендуемые величины высот долбяка, мм
|
Модуль m |
Номинальный делительный диаметр  |
Максимальная высота рабочей части долбяка  |
Высота полностью изношенного долбяка  |
|
1,00–1,50 |
80 |
18 |
4 |
|
1,75–2,50 |
80 |
20 |
5 |
|
2,75–5,00 |
80 |
21,5 |
6,5 |
|
1,00–1,50 |
100 |
19 |
4 |
|
1,75–2,50 |
100 |
23,5 |
4,5 |
|
2,75–4,00 |
100 |
28,5 |
5,5 |
|
4,50–5,00 |
100 |
29,5 |
6,5 |
|
5,50–8,00 |
100 |
32,5 |
7,5 |
 Рис.6.6 Форма ножки зуба после шлифования профиля зубьев |
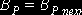
где

13. На шаге 13 производится назначение фактических величин положительного и отрицательного исходных расстояний долбяка:
а) в том случае, если выполняется условие

(то есть в тех случаях, когда сумма расчетных значений положительного исходного расстояния и абсолютной величины отрицательного исходного расстояния не превышает допустимой высоты рабочей части долбяка, рис. 6.7, а), фактические величины положительного и отрицательного исходных расстояний принимаются равными их расчетным значениям, то есть

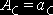
б) если сумма исходных значений положительного исходного расстояния и абсолютной величины отрицательного исходного расстояния больше максимально допустимой технологическими требованиями высоты рабочей части долбяка, то есть если имеет место неравенство

исходное расстояние долбяка располагают по одному из трех вариантов: симметрично относительно рабочей высоты долбяка, с полным использованием положительного исходного расстояния или с полным использованием отрицательного исходного расстояния, после чего производят корректировку величин исходных расстояний. Выбор того или иного варианта расположения исходных расстояний зависит от конкретных условий.
При проектировании долбяков средних модулей (m=1...5 мм), а также крупномодульных с m>5 мм и числом зубьев z0>15 принимается симметричное расположение исходного сечения (рис. 6.7, б). В этом случае фактические исходные расстояния определяются следующим образом:

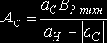
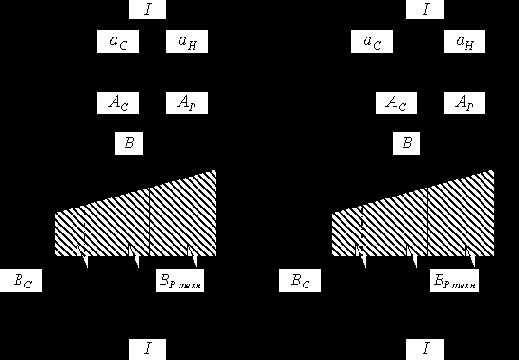
а б
Рис.6.7 Расположение исходного сечения долбяка: с полным использованием положительного и отрицательного исходного расстояния (а) и симметричное (б)
При проектировании крупномодульных долбяков (m>5 мм) с малым числом зубьев (z0<15) исходное сечение располагают с полным использованием положительного исходного расстояния (рис. 6.8, а), а фактические исходные расстояния определяют по формулам


При проектировании долбяков под шевингование, а также мелкомодульных (m<1 мм) долбяков, исходное сечение долбяка располагают с полным использованием отрицательного исходного расстояния (рис. 6.8, б), а фактические исходные расстояния определяют по формулам

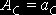

а б
Рис.6.8 Расположение исходного сечения долбяка с полным использованием положительного (а) и отрицательного (б) исходного расстояния
14. Определение размеров долбяка в плоскости его переднего торца.
В плоскости переднего торца, или, как часто говорят, в режущей плоскости, долбяк, чаще всего, представляет собой зубчатое колесо с положительным смещением исходного контура, и размеры его определяются как размеры обычного зубчатого колеса с положительным смещением. При этом выполняются следующие расчеты:
а) величина смещения исходного контура инструментальной рейки в режущей плоскости определяется по формуле

где aа0 - задний угол на вершине зуба долбяка;
б) толщина зуба долбяка по дуге делительной окружности определяется по формуле

где S0 - толщина зуба долбяка по дуге делительной окружности в исходном сечении;
в) определяется высота головки зуба долбяка в режущей плоскости. При этом используется формула:

г) определяется высота ножки зуба долбяка в режущей плоскости. Вычисление производится по формуле

д) определяется диаметр окружности вершин зубьев долбяка:

е) диаметр окружности впадин зубьев долбяка рассчитывается по формуле

Расчет по всем формулам, приведенным в п.14, производится с точностью до 0,0001 мм.
15. Определение размеров долбяка в плоскости предельной заточки.
В плоскости предельной заточки долбяк чаще всего представляет собой зубчатое колесо с отрицательным смещением исходного контура, и размеры его определяются как размеры обычного зубчатого колеса с отрицательным смещением исходного контура.
При определении размеров долбяка в плоскости предельной заточки величину отрицательного исходного расстояния следует брать с учетом его знака (то есть считать отрицательным). Вычисления производятся в следующей последовательности:
а) величина смещения исходного контура инструментальной рейки в плоскости предельной заточки определяется по формуле

б) толщина зуба долбяка по дуге делительной окружности определяется по формуле

в) высота головки зуба долбяка в плоскости предельной заточки определяется по формуле

г) высота ножки зуба долбяка в плоскости предельной заточки определяется по формуле

д) диаметр окружности вершин зубьев долбяка в плоскости предельной заточки определяется по формуле

е) диаметр окружности впадин зубьев долбяка в плоскости предельной заточки вычисляется по формуле

Расчет по всем формулам, приведенным в п.15, производится с точностью до 0,0001 мм.
16. Определение диаметра посадочного отверстия d1.
Диаметр посадочного отверстия долбяка выбирается по данным табл. 5.3 (см. С.28) и табл. 6.5 (см. С.47) в зависимости от модели зубодолбежного станка, на котором будет применяться проектируемый долбяк.
17. На шаге 17 производится назначение остальных конструктивных параметров долбяка (см. рис. 5.2, с.28). Выбираются значения следующих конструктивных параметров инструмента:
а) диаметра выточки d2;
б) диаметра опорной поверхности d3;
б) ширины ступицы b1.
Назначение величин размеров производится конструктивно с учетом соответствующих размеров стандартных дисков долбяков.
Проведенный расчет полностью определяет геометрию дискового долбяка для обработки прямозубых зубчатых колес и достаточен для назначения технических требований на инструмент (см. раздел 7, с.67) и выполнения его рабочего чертежа.
Назначение и типы зуборезных долбяков
Зуборезные долбяки относятся к достаточно широкому классу инструментов, предназначенных для обработки зубчатых клес. Долбяк представляет собой режущий инструмент, выполненный в виде зубчатого колеса с прямыми или косыми (винтовыми) зубьями, снабженного соответствующими углами резания (положительными передним и задним углами, обеспечивающими возможность обработки заготовки). Долбяки предназначаются для нарезания зубьев цилиндрических колес методом центроидного огибания, при этом центроидами зубчатого колеса и инструмента являются окружности[1]. Таким образом, для правильной обкатки необходимо, чтобы окружные скорости на начальных окружностях долбяка и нарезаемого колеса были равны между собой.
 Рис.1.1 Схема обработки долбяком прямозубого зубчатого колеса |
При обработке прямозубых колес главным движением резания для долбяка является прямолинейное возвратно-поступательное движение DГ (рис.1.1). Подача (обкат инструмента и заготовки) осуществляется путем относительного вращения долбяка (движение DW0) и заготовки (движение DW1) вокруг их осей. Во избежание повреждения уже обработанной поверхности, во время холостого хода долбяка стол с заготовкой отводится от инструмента, что создает необходимый зазор для свободного прохода зубьев долбяка (возвратно–поступательное движение DS01). Перед началом резания стол автоматически возвращается в первоначальное положение. Вращение долбяка и заготовки происходит непрерывно как в течение рабочего, так и холостого ходов.
Кроме указанных основных движений – главного движения резания DГ и движения подачи, долбяк получает радиальную подачу DS02 при врезании в заготовку до получения требуемых размеров зубьев нарезаемого колеса.
 Рис.1.2 Схема обработки долбяком косозубого зубчатого колеса |
При обработке долбяком косозубого колеса (рис. 1.2), главное движение резания является винтовым возвратно–поступательным движением, которое представляет собой геометрическую сумму движений DГ1 и DГ2. В остальном процесс обработки аналогичен рассмотренному выше процессу обработки прямозубого зубчатого колеса.
Общая схема операции нарезания зуб чатого колеса зуборезным долбяком представлена на рис. 1.3.
При нарезании зубьев долбяком имеет место прерывистый процесс резания и профилирования, поэтому профиль зубьев, образованный в процессе обработки, имеет огранку в поперечном направлении. Однако ввиду независимости скоростей главного движения резания и движения обката огранка может быть уменьшена, и, практически, отклонения получаются незначительными.
Таким образом, зубодолбежный станок для осуществления процесса обработки должен иметь следующие движения [20, с.354]:
1) возвратно-поступательное движение рабочего шпинделя с долбяком (DГ, DГ1) и возвратно-вращательное движение шпинделя (DГ2);
2) вращательное движение рабочего шпинделя (DW0);
3) вращательное движение стола с заготовкой (DW1);
4) отвод стола во время холостого хода долбяка (DS01)
5) радиальное движение подачи долбяка (DS02);
6) автоматические движения для подачи долбяка на установленную глубину резания и отвода стола после окончания обработки.
Следует указать, что долбяки являются наиболее универсальными инструментами для нарезания зубьев цилиндрических колес. Ими можно нарезать любое зубчатое колесо, если оно может быть нарезано каким–либо другим зуборезным инструментом. Специфическими областями применения долбяков являются следующие: нарезание зубьев «в упор» на так называемых блочных колесах и на колесах с буртами (рис. 1.4, а); нарезание колес внутреннего зацепления; нарезание шевронных колес с непрерывным зубом без канавки для выхода инструмента (рис. 1.4, б); нарезание точных зубчатых реек методом огибания и т.д.
По производительности обработки долбяк стоит несколько выше, чем гребенка (что обеспечивается благодаря непрерывному процессу резания) и несколько уступает червячной зуборезной фрезе.
Однако, в ряде случаев долбяки могут обеспечить более высокую производительность, чем фрезы, например, при нарезании зубчатых секторов, колес с узким ободом и большим числом зубьев и др. Вопрос о целесообразности применения долбяков в тех случаях, когда возможно нарезание зубьев также червячными фрезами, должен решаться для каждого случая отдельно путем сравнения машинных времен.
По точности обработки нарезаемых колес долбяк может конкурировать с гребенкой, например, в отношении погрешности эвольвентного участка профиля. Однако в отношении шага зубьев долбяк не является совершенным инструментом. [20, с.355]. В процессе обработки последовательные зубья колеса нарезаются последовательными зубьями долбяка, поэтому суммарная ошибка шага зубьев долбяка, вследствие накопления ошибки, с неизбежностью отражается на точности шага между первым и последним нарезанными зубьями. С точки зрения этого параметра, гребенка и червячная фреза находятся в несколько лучших условиях и обеспечивают более высокую точность.

Рис.1.3 Схема нарезания зубчатого колеса зуборезным долбяком


а б
Рис.1.4 Специфические случаи обработки зубчатых колес долбяком: обработка «в упор» (а); обработка шевронного зубчатого колеса с непрерывным зубом (б)
Так же, как и иные классы инструмента, применяемого в современном машиностроении, зуборезные долбяки можно разделить на группы по различным признакам (рис. 1.5, 1.6). По конструктивной форме долбяки делят на дисковые (рис. 1.6, а, в), чашечные (рис. 1.6, б) и втулочные. Дисковые долбяки применяются для нарезания обычных прямозубых цилиндрических зубчатых колес, главным образом наружного зацепления. Базой для крепления дисковых долбяков является отверстие, а также наружная и внутренняя опорные плоскости. При помощи отверстия долбяк устанавливается точно по центру оси шпинделя зубодолбежного станка, а опорные плоскости обеспечивают перпендикулярное к оси шпинделя положение режущих кромок и совпадение направлений осей долбяка и шпинделя [20, с.358].

Рис.1.5 Схема классификации зуборезных долбяков
Чашечные долбяки применяются для нарезания наружных блочных колес «в упор» и для изготовления внутренних колес средних модулей. Они отличаются от дисковых более глубокой выточкой, необходимой для размещения крепежной гайки или головки крепежного винта. При обработке блочных шестерен в ряде случаев гайка или головка винта не должна выступать за плоскость, проходящую через вершинные режущие кромки. Чашечные долбяки закрепляются таким же образом, как и дисковые, с той только разницей, что гайка или болт у них помещены в теле долбяка. Втулочные долбяки закрепляются на шпинделе станка при помощи внутренней резьбы и базируются по отверстию и опорному торцу.
При классификации по способу крепления на станке дисковые, чашечные и втулочные долбяки относят к классу насадных инструментов (рис. 1.6, а?в). Хвостовые долбяки (рис. 1.6, г) имеют разнообразные способы крепления, однако наиболее распространенной конструкцией является хвост с конусом Морзе, снабженный центровыми отверстиями. По центровым отверстиям на хвостовике долбяка производится базирование в процессе изготовления и заточки инструмента. Хвостовые долбяки применяются для нарезания колес внутреннего зацепления и мелкомодульных колес.
При классификации по направлению зубьев выделяются прямозубые, косозубые, а также косозубые парные долбяки. Прямозубые долбяки (рис. 1.6, а, б, г) применяются для нарезания прямозубых колес. Косозубые и косозубые парные (рис. 1.4, б; рис. 1.6, в) используются при обработке соответственно косозубых и шевронных колес.
По конструкции самого инструмента зуборезные долбяки делятся на цельные, составные и сборные. В конструкциях сборных и составных долбяков при изготовлении зубьев инструмента, как правило, используются твердосплавные пластины [8, с.51?57][2]. Долбяки, в конструкциях которых используется твердый сплав, применяются при обработке высокоточных зубчатых колес и обеспечивают достаточно высокие показатели производительности и стойкости.
Применение долбяков, оснащенных пластинами из твердых сплавов ВК15, ВК20, В12Та, позволяет повысить стойкость инструмента по сравнению с долбяками из быстрорежущей стали в 1,5 раза при скорости резания 30 м/мин; в 2-4 раза при скорости резания 40 м/мин; в 13-22 раза при скорости резания 53 м/мин. При работе со скоростями до 20 м/мин, твердосплавные долбяки практически не имеют преимуществ перед долбяками из быстрорежущей стали.


а б


в г
Рис.1.6 Основные типы зуборезных долбяков: дисковый (а), чашечный (б), для обработки косозубых колес (в), хвостовой долбяк (г)
Оформление рабочего чертежа долбяка и расчетно-пояснительной записки
Рабочий чертеж зуборезного долбяка рекомендуется выполнять на чертежной бумаге, как правило, формата А3 (297*420 мм) в соответствии с требованиями государственных стандартов ЕСКД черным карандашом или тушью. Следует помнить, что размер потребительского формата листа больше стандартного. Поэтому на потребительском формате сначала тонкой линией намечают стандартный формат, а затем, отступая 20 мм слева и по 5 мм с других сторон, проводят рамку контурной (основной) линией.
Две проекции долбяка обязательно вычерчиваются в масштабе 1:1. На этих проекциях указывают конструктивные и геометрические параметры долбяка: диаметр окружности вершин зубьев в плоскости переднего торца da0P, делительный диаметр d0, диаметр выточки d2, диаметр посадочного отверстия d1, диаметр опорного торца d3, величину положительного исходного расстояния АP, высоту долбяка B, ширину ступицы b1, передний и задний угол на вершине зуба долбяка и другие параметры.
Схематично изображается профиль зубьев долбяка в режущей плоскости, на котором указывают длину периферийной режущей кромки Sa0P, толщину зуба по дуге делительной окружности S0P, высоту головки зуба долбяка ha0P, задний угол на боковой режущей кромке в нормальном сечении aбN0.
Отклонения формы и взаимного расположения поверхностей показываются с применением условных обозначений в соответствии с ГОСТ 2.308–79. Величины допусков и предельных отклонений приведены в ГОСТ 9323?79 и в разделе 7 (см. табл. 7.1, 7.2).
На рабочем чертеже в виде таблицы приводятся данные по характеристике долбяка (табл. 8.1).
Над основной надписью в виде текста помещают технические требования. Текст записывается сверху вниз. Каждый пункт текста имеет свой номер и записывается с новой строки. Состав и порядок изложения технических требований следующий:
1) указывается материал долбяка (если долбяк цельный) или материал режущей части крепежной (если конструкция составная или сборная);
2) указывается твердость элементов долбяка, характер термообработки, вид покрытия;
3) оговариваются отклонения формы, расположения поверхностей и т.п., которые нельзя показать условными обозначениями;
4) оговариваются отклонения размеров, для которых не указаны предельные отклонения на рабочем чертеже. Используется следующая формулировка: «Неуказанные предельные отклонения размеров: отверстий - H14, валов- h14, остальных

5) дается ссылка на государственный стандарт в отношении неуказанных технических требований, используя формулировку: «Остальные технические требования по ГОСТ 9323–79»;
6) даются указания о маркировании и клеймении.
Таблица 8.1
Параметры зуборезного долбяка
|
Характеристика долбяка |
||
|
Наименование |
Обозначение |
Числовое значение |
|
Модуль |
m |
|
|
Число зубьев |
z0 |
|
|
Профильный угол |
a0 |
|
|
Высота головки зуба в исходном сечении |
ha0 |
|
|
Толщина зуба по дуге делительной окружности в исходном сечении |
S0 |
|
|
Класс точности |
1) индекса проекта – КП (курсовой проект) или КР (курсовая работа);
2) двух последних цифр года защиты работы;
3) шифра кафедры по университетской классификации (шифр кафедры «Металлорежущие станки и инструменты» ? 10.29);
4) номера проекта (работы) — по списку преподавателя.
Все части обозначений разделяются тире. Например: КР?00?10.29?20.
Расчетно-пояснительная записка оформляется на листах формата А4 (210х297мм) писчей белой бумаги аккуратно от руки чернилами (шариковой ручкой) одного цвета на одной стороне листа.
Не обязательно, однако очень желательно, выполнение пояснительной записки машинописным или типографским способом, а также с помощью принтера персональной ЭВМ. При хорошем качестве бумаги допускается размещение текста на обеих сторонах листа.
Расчетно-пояснительная записка должна содержать расчет размеров долбяка, обоснование выбора тех размеров, которые не подлежат расчету, обоснование выбора материала и геометрических параметров. Изложение материала расчетно-пояснительной записки необходимо начинать с указания исходных данных.
Расчеты и обоснования должны быть конкретными, относящимися непосредственно к проектируемому инструменту. Если определение параметров долбяка производится по формуле, то вначале записывается формула в общем виде, затем подставляются числовые значения и приводится рассчитанное значение параметра. Недопустимо сразу после формулы в общем виде давать конечный результат. Все обоснования и расчеты необходимо подтверждать ссылками на соответствующие литературные источники с указанием страниц, номеров таблиц и формул и т.д. При необходимости следует приводить эскизы.
Правила оформления расчетно-пояснительной записки соответствуют общим правилам оформления авторского текстового оригинала рукописи, изложенным в работах [14; 15]. В качестве образца оформления рукописи (размещение текста на странице; нумерация разделов, рисунков, таблиц и формул; оформление подписей рисунков и заголовков таблиц; оформление списка литературных источников и т.д.) может быть использовано данное учебное пособие.
При оформлении пояснительной записки на компьютере, рекомендуется применять текстовый редактор MS Word или подобный ему. При этом рекомендуется назначать следующие режимы форматирования:
1. Формат страницы: левое поле - 30 мм, правое поле - 20 мм, верхнее поле - 20 мм, нижнее поле - 20 мм.
2. Оформление текста: заголовок раздела - гарнитура Arial или Helvetica, 14 pt, интервал разреженный на 1-3 pt; заголовок подраздела - гарнитура Arial или Helvetica, 14 pt, без разрядки; подрисуночная подпись - гарнитура Times или Times New Roman, 14 pt, курсив; обычный текст и заголовки таблиц - гарнитура Courier New, 14 pt.
3. При оформлении текста следует использовать межстрочный интервал (интерлиньяж) 1,5 линии (18 pt) и двустороннюю выключку (выравнивание). Заголовки таблиц следует выполнять с выключкой по центру страницы. Величина отступа красной строки (абзацной втяжки) - 1?1,5 см.
4. При создании формул следует руководствоваться следующими правилами:
а) абзацы, в которых размещаются формулы, форматировать с выключкой по центру абзаца, справа размещать номер формулы;
б) стили при работе в MS Equation Editor определить на основании рекомендаций табл. 8.2;
в) размеры символов определить следующим образом:
обычный....................... 14 pt;
крупный индекс.................... 9 pt;
мелкий индекс..................... 7 pt;
крупный символ.................... 20 pt;
мелкий символ.................... 14 pt.
Таблица 8.2
Определение стиля формул
при работе в MS Equation Editor
|
Стиль |
Шрифт |
Полужирный |
Курсив |
|
Текст |
Times New Roman |
Нет |
Нет |
|
Функция |
Times New Roman |
Нет |
Нет |
|
Переменная |
Times New Roman |
Нет |
Да |
|
Греческие |
Symbol |
Нет |
Нет |
|
Символ |
Symbol |
Нет |
Нет |
|
Матрица-вектор |
Times New Roman |
Да |
Нет |
|
Числа |
Times New Roman |
Нет |
Нет |
Определение дополнительных параметров зубчатых колес
Задача расчета зубчатой передачи достаточно часто встречается в расчетных методиках, использующихся при проектировании сложнорежущего инструмента. Проектирование практически любого зуборезного инструмента предполагает необходимость полного или частичного расчета зубчатой передачи. Принимая во внимание этот факт, целесообразно детально рассмотреть последовательность расчета зубчатой передачи, которая регламентируется ГОСТ 16532?70 «Передачи зубчатые цилиндрические. Расчет геометрии» [12, с.77?118].
Как правило, исходные данные к проектированию долбяка или иного зуборезного инструмента включают чертеж зубчатого колеса, подлежащего обработке (или таблицу исходных данных, описывающих это колесо). Однако в большинстве случаев (при обработке корригированных колес), для проведения расчетов, помимо значений параметров, описывающих обрабатываемое колесо, для проектирования инструмента необходимы значения параметров, описывающих колесо, сопряженное в передаче с обрабатываемым. Полная спецификация исходных данных, необходимых для расчета зубчатой передачи, приведена в табл. 6.1.
Значительная часть исходных данных для расчета определяется путем задания параметров исходного контура обрабатываемого зубчатого колеса. Параметры исходного контура цилиндрических эвольвентных зубчатых передач определяются ГОСТ 13755-81 [1]. Схема исходного контура согласно ГОСТ 13755-81 приведена на рис. 6.2.
Согласно требованиям ГОСТ 13755-81, значения параметров исходного контура, приведенные в табл. 6.1, могут быть изменены в случаях, когда к зубчатым передачам предъявляются особые требования. Модификация исходного контура применяется для улучшения работоспособности тяжелонагруженных и высокоскоростных цилиндрических зубчатых передач внешнего зацепления. При этом в качестве линии модификации используется отрезок прямой линии (см. рис. 6.2), а значение коэффициента высоты модификации

Основные исходные данные для геометрического расчета зубчатой передачи
|
Обозначение параметра |
Наименование параметра |
Примечания |
|
z1 |
Число зубьев шестерни (меньшего зубчатого колеса) |
|
|
z2 |
Число зубьев колеса (большего зубчатого колеса) |
|
|
m |
Модуль колес передачи, мм |
|
|
b |
Угол наклона линии зуба, град. |
Задается для косозубых передач. Для прямозубых передач b=0° |
|
a |
Угол профиля исходного контура, град. |
При использовании стандартного исходного контура согласно ГОСТ 13755-81 принимается a=20° |
 |
Коэффициент высоты головки зуба колеса |
При использовании стандартного исходного контура согласно ГОСТ 13755-81 принимается  |
 |
Коэффициент граничной высоты |
Граничная высота - расстояние между окружностью вершин зубьев цилиндрического зубчатого колеса и концентрической окружностью, проходящей через граничные точки профилей зубьев. Для исходного контура по ГОСТ 13755-81 принимается  |
 |
Коэффициент радиального зазора в передаче |
В большинстве случаев расчета может быть принято  |
|
b |
Ширина зубчатого венца |
Параметр необходим при расчете контрольных размеров косозубых колес |

Рис. 6.2. Исходный контур согласно ГОСТ 13755-81
Значение коэффициента глубины модификации D* выбирается в зависимости от модуля зубчатого колеса и степени точности по нормам плавности работы. Полные данные к определению коэффициента глубины модификации профиля представлены в [23, с.49-52, табл. 3.3-3.6]. В табл. 6.2 приведены дополнительные исходные данные, которые необходимы при геометрическом расчете зубчатых передач с модифицированным зубом, а также при расчете корригированных зубчатых передач.
Таблица 6.2
Дополнительные исходные данные для геометрического расчета зубчатой передачи
|
Дополнительные параметры для колес с модифицированными зубьями |
||
|
Форма головки зуба колеса согласно ГОСТ 13755-81 [1] (вид модификации) |
При наличии модификации головки зуба дополнительно задаются коэффициенты высоты и глубины модификации |
|
 |
Коэффициент глубины модификации профиля головки зуба колеса |
|
 |
Коэффициент высоты модификации профиля головки зуба колеса |
|
|
Дополнительные параметры для корригированных колес |
||
 |
Межосевое расстояние, мм |
Для полного однозначного определения зубчатой передачи достаточно задания любых двух |
|
x1 |
Коэффициент смещения шестерни (меньшего колеса) |
из группы параметров, входящих в комплект дополнительных параметров для корригированных колес (x1
и x2; aw
и x1 или aw и x2). В случае, |
|
x2 |
Коэффициент смещения колеса (большего колеса) |
если задано только межосевое расстояние, рассчитывается коэффициент суммы смещений, который затем разбивается на x1
и x2. |
|
Дополнительные параметры для контроля качества зацепления по геометрическим показателям |
||
|
ea min |
Минимально допустимая величина коэффициента торцового перекрытия |
Для прямозубых передач рекомендуется ea min=1,2. Для косозубых передач рекомендуется ea min=1,0. |
|
eb min |
Минимально допустимая величина коэффициента осевого перекрытия |
Задается только для косозубых передач. Рекомендуется eb min=1,0 |
|
s*na min |
Минимально допустимый коэффициент нормальной толщины зубьев на поверхности вершин |
При однородной структуре материала зубьев рекомендуется s*na min =0,3; при поверхностном упрочнении зубьев рекомендуется s*na min =0,4 |
На рис. 6. 3 представлена схема, иллюстрирующая общую последовательность расчета геометрии зубчатой передачи [12, с.78]. Числами в блоках приведенной диаграммы указаны номера шагов алгоритма расчета зубчатой передачи, который изложен ниже. Все вычисления в приведенном ниже алгоритме производятся с точностью до 0,0001 мм для линейных величин или 0,0001° (0,1²) для угловых величин. Окончательные результирующие значения могут быть округлены до технологически приемлемой точности (как правило, 0,01-0,001 мм и 1²).
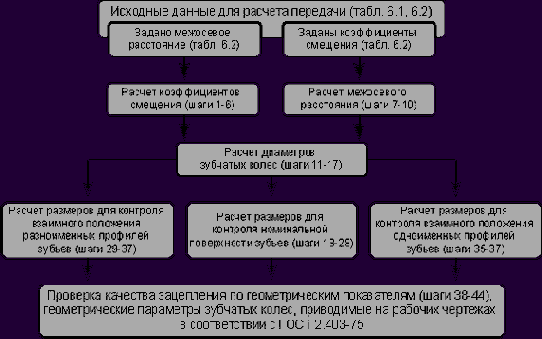
Рис.6.3 Принципиальная схема расчета геометрии зубчатой передачи
Ниже представлен общий алгоритм расчета геометрических параметров зубчатой передачи ГОСТ 16532?70. В алгоритме опущены этапы расчета контрольных размеров по шарикам (роликам) и толщины по хорде на окружности произвольного диаметра. Все остальные этапы расчета приводятся полностью. Выбор метода контроля зубчатых колес ГОСТ 16532?70 не регламентируется, поэтому при проведении расчета следует определить, какую именно группу параметров следует использовать при контроле зубчатой передачи. Выбор группы контрольных параметров иллюстрируется схемой на рис. 6.3. Алгоритм расчета зубчатой передачи состоит из следующей последовательности вычислений:
1. Если задано межосевое расстояние aw, производится расчет коэффициентов (коэффициента) смещения (шаги 2-6). Если заданы коэффициенты смещения - расчет начинается с шага 7.
2. Определяется делительное межосевое расстояние зубчатой передачи a:

3. Рассчитывается торцовый угол профиля передачи at:

4. Рассчитывается угол зацепления передачи atw:

Угол зацепления atw - это острый угол в главном сечении эвольвентной зубчатой передачи между линией зацепления и прямой, перпендикулярной к межосевой линии.
5. Определяется коэффициент суммы смещений:

Напомним, что эвольвентный угол inv(j) - функция, которая определяется следующим образом:

где j представлена в радианах.
6. Коэффициент суммы смещений разделяется на два слагаемых - коэффициенты смещения шестерни x1 и колеса x2. В случае, если один из коэффициентов смещений колес задан, второй определяется вычитанием его величины из коэффициента xS. Если оба коэффициента смещения неизвестны, разбивка xS на слагаемые проводится с учетом требований отсутствия интерференции, подрезания, заострения зубьев. Для определения коэффициентов смещения могут использоваться рекомендации [12, C.105?107] или блокирующие контуры [12, C.109?111]. После задания коэффициентов смещения, удовлетворяющих требованиям отсутствия интерференции, подрезания, заострения зубьев, и обеспечивающих выполнение равенства

расчет продолжается с шага 11.
7. Если в комплект исходных данных включены коэффициенты смещения x1 и x2, расчет начинается с определения коэффициента xS:
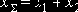
8. Рассчитывается торцовый угол профиля передачи at:

9. Рассчитывается инволюта угла зацепления atw:

По величине инволюты (эвольвентного угла) inv(atw) определяется угол зацепления atw. Определение atw не может быть выполнено аналитически и требует проведения подбора или применения численных методов. Метод численного определения величины угла по значению его инволюты детально изложен в [23, с.93?96].
10. Определяется межосевое расстояние передачи aw:

11. На шагах 11?17 определяются диаметры зубчатых колес, входящих в передачу: делительные, начальные, диаметры окружностей вершин и впадин. Делительные диаметры колес определяются по формулам


12. Передаточное число u рассчитывается по формуле

13. Диаметры начальных окружностей шестерни и колеса рассчитываются по формулам


14. Коэффициент воспринимаемого смещения рассчитывается по формуле
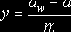
15. Коэффициент уравнительного смещения рассчитывается по формуле

16. Диаметры вершин зубьев шестерни и колеса рассчитываются по формулам


17. Диаметры впадин зубьев шестерни и колеса рассчитываются по формулам


Следует указать, что в обоснованных случаях допускается устанавливать значения диаметров вершин и впадин, несколько отличающиеся от расчетных значений. В практических ситуациях назначаются величины da и df, обеспечивающие удобство изготовления и контроля зубчатых колес.
18. На шагах 18?28 рассчитываются размеры для контроля номинальной поверхности зуба: основные диаметры, углы профиля зубьев на окружности вершин, радиусы кривизны профилей зубьев в нижней точке и т.д. Диаметры основных окружностей зубчатых колес определяются по следующим формулам:


19. Углы профиля зубьев шестерни и колеса в точках на окружностях вершин рассчитываются по формулам


Следует иметь в виду, что при расчете углов профиля зубьев на окружностях вершин следует подставлять в формулу действительные (принятые) диаметры окружностей da1 и da2. В случае, если на вершине зубьев колеса имеется притупление, следует подставлять в формулу диаметр окружности притупления, принимаемый по конструктивным соображениям.
20. Радиусы кривизны активного профиля зубьев шестерни и колеса в нижних точках рассчитываются по формулам


21. Угол развернутости активного профиля зуба в нижней точке для шестерни и колеса рассчитывается по формулам


22. В случае, если модификация головок зубьев колес не производится, осуществляется переход к шагу 28 алгоритма. Если модификация осуществляется и линия модификации - прямая, производится дополнительный расчет (шаги алгоритма 22?27).
Определяются радиусы кривизны профилей зубьев в начальных точках линии модификации для шестерни и колеса:


23. Определяется углы развернутости профилей зубьев шестерни и колеса, соответствующие начальным точкам модификации головки:


24. Определяются диаметры окружностей модификации головок зубьев:


25. Определяется угол линии модификации головки торцового исходного контура в начальной точке модификации. Используется следующая формула:

26. Рассчитываются диаметры основных окружностей эвольвент, являющихся линиями модификации головок зубьев для шестерни и для колеса:


27. По приближенной формуле рассчитывается нормальная глубина модификации торцового профиля головки зуба для шестерни и для колеса:


28. После выполнения дополнительного расчета для модифицированных зубьев, производится расчет размера для контроля контактной линии поверхности зуба. Рассчитывается основной угол наклона (угол наклона винтовой линии зуба на основном цилиндре):

29. Шаги алгоритма 29?34 связаны с расчетом размеров для контроля взаимного положения разноименных профилей зубьев.
Рассчитываются величины постоянной хорды для шестерни и колеса по следующим формулам:


Напомним, что постоянной хордой зуба

Для того, чтобы проведенный расчет был корректным (и, соответственно, для того, чтобы проектируемая передача была геометрически и технологически осуществима), как для шестерни, так и для колеса, должны выполняться условия вида:

где rs - радиус кривизны разноименных профилей зубьев в точках, определяющих постоянную хорду, который может быть определен по формуле

При модификации головки должно выполняться дополнительное условие

Приведенные неравенства должны выполняться как для шестерни, так и для колеса. В практическом расчете в формулы (6.30)?(6.32) должны поочередно подставляться величины радиусов, диаметров и длин, соответствующие шестерне и колесу.
30. Определяется высота до постоянной хорды для шестерни и колеса. При этом используются формулы:.


31. Помимо величины постоянной хорды и высоты до нее, может также производиться расчет длины общей нормали. Для расчета длины общей нормали вычисляется угол профиля в точке на концентрической окружности диаметра dx=d+2xm (при расчете для шестерни и для колеса в приведенные ниже формулы подставляются соответствующие индексы - «1» или «2» соответственно):

32. Определяется расчетное число зубьев в длине общей нормали:

Расчетное число зубьев в длине общей нормали zWr округляется до ближайшего целого значения zW.
33. Рассчитывается длина общей нормали W на zW зубьях:

Для того, чтобы выполненный расчет был корректным, требуется выполнение условия

где rW - радиус кривизны разноименных профилей зуба в точках, определяющих длину общей нормали, а ra - радиус кривизны профиля зуба в точке на окружности вершин:


Если условие левой части неравенства не выполняется, следует пересчитать значение W при увеличенном значении zW. Если не выполняется условие правой части неравенства - W пересчитывается при уменьшенном значении zW. При увеличении или уменьшении числа зубьев в длине общей нормали zW ее величина W соответственно увеличивается или уменьшается на величину шага зацепления pa.
Для косозубых колес должно выполняться дополнительное условие:

где b - ширина венца зубчатого колеса.
34. Определяется нормальная толщина зубьев шестерни и колеса. При этом используются формулы:


35. Шаги алгоритма 35?37 связаны с расчетом размеров для контроля взаимного положения одноименных профилей зубьев.
Определяется шаг зацепления зубчатой передачи:

36. Определяется осевой шаг передачи (только для косозубых передач, для прямозубых передач осевой шаг равен бесконечности):

37. Определяется ход шестерни и колеса (только для косозубых колес, для прямозубых колес ход равен бесконечности):


38. На шагах 38?44 проводится проверка качества зацепления по геометрическим показателям. Для проверки отсутствия подрезания зуба рассчитывается коэффициент наименьшего смещения (для шестерни и колеса в приведенные ниже формулы подставляются индексы «1» и «2» соответственно):

При x ³ xmin подрезание зуба исходной производящей рейкой отсутствует.
39. Для проверки отсутствия интерференции зубьев вычисляется радиус кривизны в граничной точке профиля зуба:

При rl £ rp интерференция зубьев отсутствует. В случае, если rl<0, имеет место подрезание зубьев.
40. Рассчитывается коэффициент торцового перекрытия передачи ea по формуле

Формула справедлива, если отсутствует интерференция зубьев и верхняя точка активного профиля совпадает с точкой на окружности вершин. Условие по коэффициенту торцового перекрытия выполняется, если ea³eamin.
41. Определяется коэффициент осевого перекрытия передачи eb. Для прямозубых передач eb=0. Для косозубых передач при расчете eb используется формула:

Для косозубых передач рекомендуется (но не является строго обязательным) обеспечивать выполнение условия eb³ebmin.
42. Определяется общий коэффициент перекрытия передачи:

43. В случае, если головка исходного контура имеет модификацию, производится дополнительный расчет - определяются углы профиля зубьев в начальных точках модификации головки (для шестерни и колеса):

после чего вычисляется часть коэффициента торцового перекрытия, определяемая участками торцовых профилей зубьев, совпадающими с главными профилями:

44. Последним шагом в геометрическом расчете зубчатой передачи является проверка нормальной толщины зубьев на поверхности вершин (для шестерни и колеса). При проведении проверки определяются углы наклона линии вершины зубьев:

и вычисляются нормальные толщины зубьев на поверхностях вершин

Для корректно спроектированной передачи должно выполняться условие sna ³ (s*na min)m.
Основные задачи и общая последовательность проектирования долбяков
При проектировании долбяка необходимо обеспечить выполнение следующего требования: два колеса с любыми числами зубьев, нарезанные новым или сточенным долбяком, должны правильно зацепляться между собой. Геометрия зацепления пары «долбяк – колесо» может наложить на зацепление колес, нарезанных данным долбяком, некоторые ограничения. Они приводят к тому, что устанавливается определенный диапазон чисел зубьев колес, нарезанных данным долбяком, которые могут правильно между собой зацепляться в любых сочетаниях только в пределах этого диапазона. Принципиальная схема проектного расчета дискового долбяка представлена на рис.6.1.
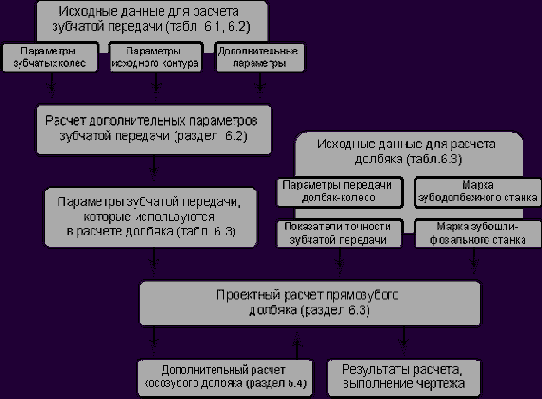
Рис.6.1 Принципиальная схема проектного расчета дискового зуборезного долбяка
Общая последовательность расчета и проектирования зуборезных долбяков состоит из двух основных этапов. На первом этапе производится определение дополнительных (не входящих в комплект исходных данных) параметров зубчатых колес (обрабатываемого и сопряженного с ним), а на втором этапе – собственно определение конструктивных и геометрических параметров долбяка. В приведенных ниже разделах подробно излагается последовательность вычислений, которые должны быть выполнены при проектирования долбяка.
При более детальном рассмотрении, проектный расчет дискового долбяка может быть представлен в виде следующей последовательности действий:
1. Определение дополнительных параметров обрабатываемых колес, необходимых для расчета долбяка.
2. Определение диаметров делительной окружности, основной окружности и числа зубьев долбяка.
3. Выбор геометрических параметров (углов резания) долбяка.
4. Определение размеров исходного контура инструментальной рейки, определяющего основные размеры зуба долбяка в исходном сечении.
5. Определение положительного и отрицательного исходного расстояния.
6. Определение высоты долбяка и уточнение положительного и отрицательного исходного расстояния.
7. Определение размеров долбяка в режущей плоскости и на пределе заточки.
8. Определение конструктивных размеров долбяка.
9. Определение данных, необходимых для изготовления долбяка.
10. Определение совокупности параметров, необходимых для контроля долбяка.
Исходными данными для проектирования зуборезного долбяка являются параметры нарезаемого зубчатого колеса и зубчатого колеса, сопряженного с ним в передаче, задаваемые чертежом, а также параметры оборудования, на котором проводится шлифовка зубьев долбяка и обработка зубчатого колеса.
Особенности конструкции зуборезных долбяков
Как отмечалось ранее, по своей конструкции долбяк представляет собой зубчатое колесо, но, в отличие от последнего, он имеет передние и задние углы на вершине и боковых сторонах зубьев, которые обеспечивают возможность резания. Для обеспечения положительных задних углов, зубья долбяка образуются путем смещения исходного контура рейки и имеют в каждом сечении, перпендикулярном к оси, свою особую величину смещения контура.
На рис. 2.1 показана схема образования задней поверхности зуба долбяка. Пусть в сечении I–I смещение исходного контура рейки равно нулю (то есть xm=0). Тогда в этом сечении долбяк будет представлять собой обычное некорригированное зубчатое колесо.

Рис.2.1 Схема образования задней поверхности зуба долбяка
В сечении II–II по передней поверхности долбяка смещение исходного контура будет положительным (+xm), а в сечении III–III ? отрицательным (?xm). Переменный сдвиг исходного контура рейки, постепенно уменьшающийся от передней поверхности к опорной, создает задний угол на вершине (aа0) и задний угол на боковых сторонах.
Таким образом, долбяк можно рассматривать как совокупность бесконечно большого количества элементарных зубчатых колес с бесконечно малой шириной обода DB®0 (рис. 2.2), имеющих соответственно положительное, нулевое и отрицательное смещение контура и закрепленных на одной оси в порядке убывания величин смещения xm. Каждое из этих элементарных колес образовано огибающим движением рейки с профильным углом a0, и поэтому любое сечение долбяка, перпендикулярное к его оси, имеет один и тот же эвольвентный профиль. По мере перетачивания долбяка в работу резания и в зацепление с нарезаемым колесом вступает одно из этих бесконечно тонких зубчатых колес с соответствующей величиной смещения исходного контура рейки. Поэтому колеса, нарезанные различными сечениями долбяка, будут иметь один и тот же эвольвентный профиль.

Рис. 2.2 Долбяк как совокупность элементарных зубчатых колес со смещением исходного контура рейки

Рис. 2.3 Исходное сечение долбяка
Рис. 2. 3 позволяет увидеть, что положительное исходное расстояние A есть расстояние от исходного сечения I–I до переднего торца долбяка (до сечения II–II). Между величиной положительного исходного расстояния и величиной смещения исходного контура рейки в сечении II–II существует зависимость:

где aа0 ? задний угол на вершине зуба долбяка.
В сечении II–II, которое называется режущей плоскостью, долбяк представляет собой зубчатое колесо с положительным смещением исходного контура рейки, и размеры его в этом сечении определяются как размеры зубчатого колеса со смещением, например:



где a0 – угол профиля долбяка.
С увеличением положительного исходного расстояния увеличивается срок службы долбяка, повышается число возможных переточек, уменьшается опасность подрезания профиля колес с малым числом зубьев и срезания вершин зубьев колес, нарезаемых долбяками с малым числом зубьев. Таковы соображения, говорящие в пользу увеличения положительного исходного расстояния. Но, с другой стороны, имеются соображения противоположного характера: с увеличением положительного исходного расстояния уменьшается длина периферийной режущей кромки или, иначе, ширина зуба долбяка на его вершине. Это отрицательно сказывается на стойкости долбяка. Кроме того, долбяки с большой величиной положительного исходного расстояния дают у основания зубьев нарезаемых колес большую высоту так называемой «исходной кривой», то есть не обеспечивают необходимую длину эвольвентного участка профиля зуба колеса. Это приводит к пересечению (интерференции) профилей зубьев сопряженных колес и к зацеплению вершинами зубьев, которое вызывает быстрый износ зубьев и крайне неравномерный ход передачи, при котором возникает сильный шум. При большом отклонении от правильного зацепления может произойти даже защемление и поломка зуба. Поэтому при проектировании долбяка сначала определяется величина положительного исходного расстояния из условия полной обработки активной части профилей зубьев колес, затем из минимально допустимой длины периферийной режущей кромки и для дальнейших расчетов берется меньшая величина положительного исходного расстояния.
На рис. 2. 3 отрицательное исходное расстояние есть расстояние от исходного сечения I–I до предела заточки долбяка (сечение IV–IV). Между величиной отрицательного расстояния и величиной смещения исходного контура рейки в сечении IV–IV существует зависимость:

На пределе заточки долбяк, чаще всего, представляет собой зубчатое колесо с отрицательным смещением исходного контура рейки, и размеры его в этом сечении определяется как размеры зубчатого колеса со смещением, например:



С увеличением отрицательного исходного расстояния увеличивается число возможных переточек и срок службы долбяка, увеличивается длина периферийной режущей кромки и стойкость долбяка, уменьшается величина исходной кривой на зубе нарезаемого колеса. Это положительные факторы. Однако увеличение отрицательного исходного расстояния лимитируется опасностью среза (при малых числах зуба) или наоборот, неполной обработкой вершин зубьев нарезаемого колеса, так как при этом эвольвентная часть зуба долбяка может получиться настолько уменьшенной, что она будет недостаточной для обработки зуба колеса по всей его высоте. При большом отрицательном исходном расстоянии может наступить и другое, более редкое нежелательное явление – подрезание зубьев нарезаемого колеса. Подрезание зубьев колеса возможно в том случае, если вершина зуба долбяка зайдет внутрь основной окружности нарезаемого колеса.
Так как конструктивные элементы долбяка (число зубьев, делительный диаметр, исходные размеры зубьев, углы резания) в большинстве случаев являются известными или задаваемыми величинами, расчет долбяка в основном сводится к определению оптимальных значений исходных расстояний для конкретных условий обработки.
Особенности проектного расчета косозубых долбяков
Методики расчета прямозубых и косозубых долбяков во многом похожи. Это, в первую очередь, объясняется тем, что так же как и прямозубый, косозубый долбяк в любом торцовом сечении представляет собой корригированное эвольвентное зубчатое колесо. Вследствие этого определение размеров косозубого долбяка в торцовом сечении производится по тем же формулам, что и для прямозубого долбяка. При этом делается поправка на то, что у прямозубого долбяка торцовое сечение совпадает с нормальным, а у косозубого долбяка эти сечения различаются.
Однако, несмотря на значительное сходство конструкции прямозубых и косозубых долбяков, последние имеют некоторые конструктивные и геометрические особенности. Так, например, в отличие от прямозубых долбяков, они имеют разные основные окружности для «острой» и «тупой» сторон зубьев, вследствие чего имеют разные профильные углы. Кроме того, имеются различия в методике расчета прямозубых и косозубых долбяков на этапах назначения числа зубьев долбяка, расчета исходных расстояний и т.д. В данном разделе излагаются основные отличия методики расчета косозубого долбяка от «базовой» методики расчета, которая была изложена в предыдущем разделе. Наиболее значимые различия в методиках проектирования прямозубого и косозубого долбяков проявляются на следующих этапах [18, 21]:
1. Назначение числа зубьев и делительного диаметра долбяка (см. шаг 1 алгоритма, с.46). При проектировании косозубого долбяка в формуле для определения числа зубьев учитывается шаг PZ имеющегося винтового копира к зубодолбежному станку. При этом используется формула:

где m - нормальный модуль передачи, b0 - угол наклона зубьев долбяка. Номинальный делительный диаметр долбяка определяется по той же формуле, что и делительный диаметр зубчатого колеса (см. С.36):


Рис. 6.9 Схема к определению геометрических параметров косозубого долбяка
2. Расчет фактического (корректированного) угла профиля (см. шаг 6 алгоритма, с.51). При расчете прямозубого долбяка рассчитывается корректированный угол профиля a0K, который одинаков для правой и левой стороны зуба. При расчете косозубого долбяка, корректированный угол профиля рассчитывается отдельно для острой и тупой стороны зуба долбяка (a0K ост и
a0K туп соответственно) [20, с.499]. Схема к определению геометрических параметров косозубого долбяка представлена на рис. 6.9. При расчете используются следующие формулы:


где b0 ост и b0 туп - фактические (инструментальные) углы наклона линии зуба долбяка на «острой» и «тупой» стороне профиля, которые рассчитываются по следующим формулам [20, с.496]:


Углы aб0 ост и aб0 туп - это боковые задние углы в на «острой» и «тупой» стороне профиля в сечении по делительному цилиндру, которые определяются по следующим формулам:


3. При расчете прямозубого долбяка боковой задний угол на поверхности делительного цилиндра aб0 рассчитывается на шаге 7, б алгоритма (см. С.51). При расчете косозубого долбяка этот угол вычисляется при определении корректированного угла профиля. Остальные геометрические параметры, относящиеся к боковым режущим кромкам для косозубого долбяка определяются так же, как и для прямозубого. Однако в каждом случае рассчитываются не один, а два значения параметров - для «острой» и «тупой» стороны зуба долбяка (см. формулы на С.51).
4. При проектировании прямозубого долбяка производится вычисление фактического диаметра основной окружности (см. шаг 8 алгоритма, с.51). При проектировании косозубого долбяка диаметр основной окружности рассчитывается для острой и тупой стороны зуба:


5. Расчет положительного исходного расстояния.
При проектировании косозубого долбяка для расчета положительного исходного расстояния используются следующие формулы:
а) при расчете положительного исходного расстояния, обеспечивающего полную обработку рабочей части профиля зуба колеса (см. шаг 10, а алгоритма, с.53), используется следующая формула:

где C - вспомогательная величина, которая для косозубых долбяков определяется следующим образом:

б) при расчете положительного исходного расстояния, регламентируемого заострением зуба долбяка (см. шаг 10, б алгоритма, с.53), используется следующая формула:

6. Расчет отрицательного исходного расстояния. При проектировании косозубого долбяка для расчета отрицательного исходного расстояния используются следующие формулы:
а) при расчете отрицательного исходного расстояния, при котором гарантируется отсутствие среза на головках зубьев колес или неполной обработки головок зубьев (см. шаг 11, а алгоритма, с.54), используется следующая формула:

б) При расчете отрицательного исходного расстояния предельно сточенного долбяка, при котором будет происходить начало подрезания ножек зубьев нарезаемых колес (см. шаг 11, б алгоритма, с.54), используется формула:

Изложенные в данном разделе дополнения к методике проектирования достаточны для выполнения проектного расчета косозубого долбяка, конструкция которого близка к конструкции стандартного долбяка. В случае проектирования долбяка, к которому предъявляются специальные требования, методика расчета может быть изменена или дополнена.
Стандартные конструкции зуборезных долбяков
Стандартные зуборезные долбяки рассчитаны на условия нарезания зубчатых колес в диапазоне чисел зубьев от 17 до 120. Чистовые мелкомодульные зуборезные долбяки (дисковые и хвостовые) модулей 0,14—0,9 мм представлены в ГОСТ10059—80Е. Детальные данные о конструкциях мелкомодульных зуборезных долбяков типа 1 и типа 2 согласно ГОСТ 10059—80Е приведены в [21, с.600]. В табл. 5.1 представлены рекомендованные ГОСТ 10059—80Е ряды модулей и чисел зубьев для мелкомодульных долбяков. Чистовые зуборезные прямозубые и косозубые долбяки (дисковые, чашечные и хвостовые) модулей 1—12 мм представлены в ГОСТ 9323—79*. Основные размеры различных типов долбяков с номинальными делительными диаметрами 25?200 мм приведены в табл.5.2.
Стандартные зуборезные долбяки изготовляют трех классов точности: АА, А и В. Долбяки класса точности АА предназначены для нарезания колес 6-ой степени точности, а классов А и В – соответственно для колес 7?ой и 8?ой степеней точности.
Таблица 5.1
Рекомендованные конструктивные параметры долбяков зуборезных мелкомодульных дисковых типа 1 и типа 2 согласно ГОСТ 10059?80Е
| Параметр | Обозначение | Стандартный ряд значений |
| Дисковые долбяки (тип 1), рис. 5.1, а, б | ||
| Модуль долбяка, мм | m | 0,14; 0,15; 0,19; 0,20; 0,22; 0,25; 0,28; 0,30; 0,35; 0,40; 0,45; 0,50; 0,55; 0,60; 0,70; 0,80; 0,90 |
| Делительный диаметр, мм | d0 | 40; 63 |
| Число зубьев | z0 | 320; 290; 266; 256; 228; 222; 212; 200; 182; 160; 144; 140; 132; 128; 116; 114; 108; 100; 90; 80; 72; 66; 56; 50; 44 |
| Хвостовые долбяки (тип 2), рис. 5.1, г | ||
| Модуль долбяка, мм | m | 0,1; 0,11; 0,12; 0,14; 0,15; 0,18; 0,20; 0,22; 0,25; 0,28; 0,30; 0,35; 0,40; 0,45; 0,50; 0,55; 0,60; 0,70; 0,80; 0,90 |
| Делительный диаметр, мм | d0 | 12; 16; 25 |
| Число зубьев | z0 | 256; 228; 200; 182; 160; 144; 132; 128; 126; 114; 108; 100; 90; 84; 80; 72; 67; 64; 58; 56; 50; 45; 44; 40; 36; 32; 30; 28; 25; 24; 23; 20 |
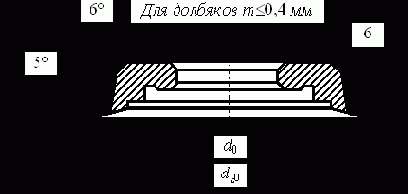
а

б
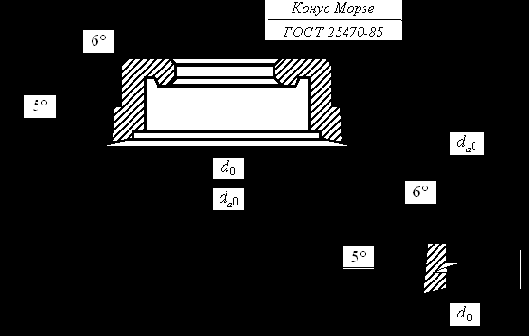
в г

Рис.5.2 Основные конструктивные параметры дисковых долбяков
Таблица 5.3
Основные конструктивные параметры
стандартных дисковых долбяков, мм
|
Модуль m0 |
Номиналь-ный диаметр d0 |
Диаметр посадочного отверстия d1 |
Диаметр выточки d2 |
Диаметр опорной поверхности d3 |
Ширина ступицы b1 |
Высота долбяка B |
|
1,0–1,5 |
80 |
31,75 |
50 |
60 |
8 |
12 |
|
1,75–2,5 |
80 |
31,75 |
50 |
60 |
8 |
15 |
|
2,75–5,0 |
80 |
31,75 |
50 |
60 |
8 |
17 |
|
1,0–1,75 |
100 |
44,45 |
70 |
80 |
8 |
17 |
|
2,0–5,0 |
100 |
44,45 |
70 |
80 |
10 |
20 |
|
5,5–8,0 |
100 |
44,45 |
70 |
80 |
12 |
22 |
|
2,0–3,5 |
125 |
44,45 |
80 |
90 |
10 |
22 |
|
3,75–4,5 |
125 |
44,45 |
80 |
90 |
10 |
24 |
|
5,0–10,0 |
125 |
44,45 |
80 |
90 |
14 |
28 |
|
6,0–7,0 |
160 |
88,9 |
120 |
100 |
16 |
30 |
|
8,0–10,0 |
160 |
88,9 |
120 |
100 |
20 |
32 |
|
8,0–12,0 |
200 |
101,6 |
140 |
25 |
40 |
Технические требования
При оформлении рабочего чертежа зуборезного долбяка необходимо руководствоваться техническими требованиями, которые изложены в ГОСТ 9323–79*. Некоторые положения этих требований приведены ниже:
1) долбяки должны изготавливаться из быстрорежущей стали марок, указанных по ГОСТ 19265–73;
2) твердость долбяков должна быть — HRCэ 62…65;
3) шероховатость поверхности долбяков по ГОСТ 2789–73 не должна превышать значений, указанных в табл. 7.1 (см. [21, с.607]);
4) допуски и предельные отклонения проверяемых параметров долбяков не должны превышать величин указанных в табл. 7.2;
5) неуказанные предельные отклонения размеров H14, валов h14, остальных

6) на внешней опорной поверхности каждого долбяка должны быть четко нанесены: товарный знак предприятия-изготовителя, обозначение долбяка, модуль, число зубьев, угол профиля, обозначение класса точности, марка материала, год выпуска.
Параметры шероховатости поверхностей
зуборезных долбяков
| Наименование поверхности | Класс точности |
Параметры шероховатости, мкм | |
| Ra | Rz | ||
| Передние и задние поверхности зубьев | АА, А | - | 1,6 |
| В | - | 2,5 | |
| Опорная поверхность дисковых и чашечных долбяков | АА, А, В | 0,16 | - |
| Посадочное отверстие дисковых и чашечных долбяков | АА | 0,16 | - |
| А и В | 0,25 | ||
| Внутренняя опорная поверхность дисковых и чашечных долбяков | АА, А и В | 0,63 | - |
| Поверхность хвостовика хвостовых долбяков | А | 0,5 | - |
| В | 0,63 | ||
| Остальные поверхности | АА, А, и В | 2,5 | - |
Таблица 7.2
Допуски и предельные отклонения проверяемых параметров зуборезных долбяков (ГОСТ 9323?79*)
| Параметр и | d0, мм | Класс | Допуски, мкм, при m0, мм | |||
| его обозначение | точности | от 1 до 3,5 |
св. 3,5 до 6 |
св. 6 до 10 |
св. 10 | |
| Отклонение от параллельности опорных поверхноcтей fx | До 50 | А В |
5 8 |
6 10 |
- | - |
| Св. 50 до 125 |
АА А В |
3 5 8 |
4 6 10 |
4 6 10 |
- | |
| Св.125 до 200 |
АА А В |
- | - | 6 8 12 |
||
| Торцовое биение передней поверхности fgt | До 50 | А В |
14 20 |
14 20 |
- | - |
| Св. 50 до 125 |
АА А В |
12 16 25 |
12 16 25 |
12 16 25 |
- | |
| Св.125 до 200 |
АА А В |
- | 20 28 40 |
20 28 40 |
20 28 40 |
|
| Биение окружности вершин зубьев frra0 | До 50 | А В |
12 20 |
16 25 |
- | - |
| Св. 50 до 125 |
АА А В |
10 16 25 |
12 20 32 |
12 20 32 |
- | |
| Св.125 до 200 |
АА А В |
- | - | 16 25 40 |
20 32 50 |
|
| Погрешность немодифицированного участка профиля ff0 | - | АА А В |
3 - 4 4 - 5 8 - 10 |
4 7 12 |
6 7 12 |
6 10 16 - 20 |
| Разность соседних окружных шагов fu0 | - | АА А В |
3 - 4 5 - 6 8 - 10 |
4 6 10 |
4 6 10 |
5 8 12 |
| Накопленная погрешность окружного шага FP0 | - | АА А В |
9 - 11 14 - 18 20 - 24 |
11 18 30 |
11 18 30 |
14 22 36 |
| Радиальное биение зубчатого венца Fr0 | До 50 | А В |
14 - 16 20 - 24 |
16 26 |
- | - |
| Св. 50 до 125 |
АА А В |
12 - 14 16 - 18 24 - 26 |
14 20 32 |
14 20 32 |
- | |
| Св.125 до 200 |
АА А В |
- | - | 18 24 36 |
20 - 40 |
Продолжение табл. 7.2
|
Параметр и |
d0, мм |
Класс |
Допуски, мкм, при m0, мм |
|||
|
его обозначение |
точности |
от 1 до 3,5 |
св. 3,5 до 6 |
св. 6 до 10 |
св. 10 |
|
|
Отклонение диаметра посадочного отверстия fd0 |
До 50 |
АА,А |
+5 |
+5 |
+5 |
- |
|
Св. 50 до 125 |
АА,А |
- |
+8 |
+8 |
+8 |
|
|
До 50 |
В |
+8 |
+8 |
+8 |
- |
|
|
Св. 50 до 125 |
В |
- |
+10 |
+10 |
+10 |
|
|
Отклонение высоты головки зуба fha0 |
- |
АА,А,В |
±25 |
±32 |
±40 |
±50 |
|
Отклонение углов переднего ±fga и заднего ±fak |
- |
АА |
±5ў |
±5ў |
±5ў |
±5ў |
|
А |
±8ў |
±8ў |
±8ў |
±8ў |
||
|
В |
±12ў |
±12ў |
±12ў |
±12ў |
Угол профиля зубьев долбяка
Угол профиля зубьев долбяка определяется в плоскости, перпендикулярной к его оси (то есть в плоскости, параллельной плоскости исходного сечения). Если бы долбяк имел передний угол при вершине ga0, равный нулю градусов, то его профильный угол a0 (индекс «0» указывает, что параметр относится к долбяку) был бы полностью идентичен с профильным углом a нарезаемого колеса. Однако долбяки, как правило, проектируются с положительными передними углами. Основной целью назначения положительного переднего угла является обеспечение возможно лучших условий резания. В случае, когда ga0>0, профильный угол долбяка a0 будет отличаться от угла профиля нарезаемого колеса a или от угла профиля проекции передней поверхности на торец нарезаемого колеса (этот угол также должен быть равен a).
Определим, каким должен быть профильный угол долбяка, для того чтобы профильный угол проекции передней поверхности совпадал с профильным углом нарезаемого колеса. Для простоты рассуждений рассмотрим «идеальный долбяк» с числом зубьев, равным бесконечности. Тогда он превратится в зуборезную рейку с прямобочным трапецеидальным зубом. На основании построений, приведенных на рис.3.1, имеем:

Из треугольников bcd и acd находим:

Затем получим:

где a - угол профиля зубьев нарезаемого колеса; a0K - профильный (корректированный) угол долбяка.
Таким образом, чтобы получить на нарезанном долбяком колесе заданный профильный угол a, долбяк должен быть изготовленным с профильным углом a0K. Однако, несмотря на эту коррекцию, профиль проекции передней поверхности долбяка на плоскость, перпендикулярную оси обрабатываемого колеса (а следовательно, и профиль зуба обрабатываемого колеса) не будут строго эвольвентными [19, с.745]. Отступление от эвольвенты обусловлено тем, что винтовая эвольвентная поверхность дает эвольвенту лишь в сечениях, перпендикулярных к оси винтового движения (оси долбяка). В сечении эвольвентной винтовой поверхности (боковой поверхности зуба) конусом (передней поверхностью долбяка) будет получена кривая, отличная от эвольвенты [23, с.15, табл. 1.1].

Рис.3.1 Определение профильного угла долбяка
Величину корректиррованного профильного угла долбяка a0K необходимо использовать во всех расчетах, когда долбяк рассматривается как геометрическое тело, так как боковые поверхности зубьев долбяка образованы огибающим движением рейки именно с профильным углом a0K. Когда же долбяк рассматривается в зацеплении с нарезаемым колесом, то в расчетах необходимо использовать величину профильного угла проекции передней поверхности долбяка на торец нарезаемого колеса, равный профильному углу последнего - a, так как огибающим движением именно этого профиля образуется зуб нарезаемого колеса.
Проектирование зуборезных долбяков» продолжает серию
Учебное пособие « Проектирование зуборезных долбяков» продолжает серию учебных пособий, подготовленных сотрудниками кафедры «Металлорежущие станки и инструменты» ВолгГТУ и посвященных изложению вопросов проектирования сложнорежущего инструмента. В пособиях этой серии, выпущенных в 1995-1999 годах, излагаются методы проектирования фасонных резцов [10], протяжного инструмента [9], червячных зуборезных фрез [23]. Данное учебное пособие входит в комплект методических материалов, необходимых студентам для выполнения курсового проекта по дисциплине «Проектирование металлорежущего инструмента». Кроме того, принимая во внимание возросшие требования к качеству выполнения дипломных проектов, рекомендуется использовать учебное пособие «Проектирование зуборезных долбяков» (наряду с иными пособиями данной серии) при выполнении дипломных проектов инженеров по специальности 1202 и выпускных работ бакалавров по направлению 5529.
Зуборезные долбяки (так же, как и зуборезные гребенки, шеверы, червячные зуборезные фрезы, ряд иных инструментов) относятся к классу инструментов, работающих по методу центроидного огибания. Геометрия зуборезного долбяка во многом напоминает геометрию обычного зубчатого колеса. В связи с этим методика проектирования зуборезного долбяка во многом аналогична как методике расчета эвольвентных зубчатых колес (см., например, [12, с.77?86]), так и методике расчета иных инструментов, работающих по методу центроидного огибания (см. [23, с.45?79]). Однако, наряду с рядом общих моментов, методика проектирования зуборезных долбяков имеет ряд принципиальных особенностей, которые делают ее изучение особо необходимым для специалистов–инструментальщиков высшей квалификации. Именно на эти особенности (в большинстве случаев связанные с изменением коэффициента коррекции по высоте долбяка) авторы обращали особое внимание при подготовке учебного пособия.
