Асинхронная электрическая машина
Самым распространенным двигателем в промышленности является асинхронный двигатель. На рис.2.10 показаны конструкция и схема включения статорных и роторных обмоток трехфазного асинхронного двигателя.
|
|

Рис.2.10. Конструкция (а) и схема включения статорных и роторных обмоток (б) трехфазного асинхронного двигателя
В неподвижном статоре расположены три катушки, создающие круговое вращающееся магнитное поле, а во вращающемся роторе – три катушки, замкнутые накоротко или на внешние сопротивления через контактные кольца и щетки. Если число катушек обмотки статора равно 3, т. е. на каждую фазу одна катушка, то за одну минуту вектор





где
D – внутренний диаметр статора.
За один период переменного тока вращающееся магнитное поле поворачивается на двойное полюсное деление 2



за время (

за 1с.-

за минуту в 60 раз больше, т. е.

где

Вращающийся магнитный поток Ф индуктирует в обмотках статора и ротора ЭДС


Так как обмотка ротора закорочена, то в ней возникает ток




е. от разности скоростей вращения магнитного поля






Относительная разность скоростей вращения поля и ротора

называется скольжением. Нетрудно видеть, что

В заторможенном режиме асинхронная машина работает в режиме трансформатора; ее схема замещения подобна схеме замещения приведенного трансформатора. Ток холостого хода асинхронной машины значительно выше, чем у трансформатора, так как в ней имеется рабочий зазор. Поэтому этот режим работы машины редко применяется.
В рабочем режиме частота





Энергетическая диаграмма работы машины имеет вид (рис.2.11):

Рис.2.11.Энергетическая диаграмма работы электрической машины.
Мощность, потребляемую из электрической сети можно определить, используя выражение:

В ротор передается электромагнитная мощность

Часть этой мощности расходуется на покрытие электрических потерь в обмотке ротора; оставшаяся часть превращается в механическую мощность

Потери в сердечнике ротора из-за малой величины частоты


где


где


Отсюда

Подставив сюда:



получаем:


Рис.2.12. Схема замещения цепи ротора.
Из рис.2.12 можем записать:

Так как




Теперь схему замещения ротора можно представить в виде (рис.2.13):
|
|

Рис.2.13. Схема замещения роторной цепи машины при вращении ротора без выделения (а) и с выделением (б) сопротивления механической мощности.
Сопротивление



а) б)
Рис.2.14 Полная схема замещения асинхронной короткозамкнутой машины (а) и ее упрощенная схема (б).
Без большой погрешности намагничивающую часть схемы можно непосредственно подключить к питающему напряжению





Определим ток фазы ротора как функцию параметров двигателя:

где

Величина


Критическое скольжение, соответствующее максимуму момента определяется дифференцированием полученного выражения по


Подставив полученное выражение в зависимость


С учетом последних двух зависимостей, выражение для M может быть представлено в виде так называемой уточненной формулы Клосса:

где

Анализ выражения механической характеристики показывает, что при








где

По выражению (2.20) на рис. 2.15 построена зависимость момента от скольжения M=F(s).

Рис. 2.15. Зависимость момента асинхронной машины от скольжения.
В реальных асинхронных машинах ЭДС






а) б)

в) г)
Рис. 2.16. Механические характеристики асинхронной машины при различных способах управления изменениями: активного сопротивления в цепи ротора (а), реактивного сопротивления в цепи статора (б), напряжения (в) и частоты (г) питающей цепи.
Максимум момента



Из характеристик рис. 2.16a видно, что при пуске двигателя выгодно иметь большое сопротивление


Модуль жесткости рабочего участка механической характеристики обратно пропорционален величине

При введении в цепь ротора добавочных индуктивных сопротивлений, уменьшаются величины



В пределах рабочего участка механической характеристики асинхронной машины, когда ток статора существенно не превышает номинальное значение, ЭДС двигателя E незначительно отличается от напряжения сети:

Из этого выражения следует, что при






При










увеличение

При необходимости уменьшения частоты



Устойчивость работы электродвигателя – способность двигателя восстанавливать установившуюся скорость вращения при небольших кратковременных возмущающих воздействиях (по питающей сети, по моменту нагрузки).
Условие равновесия моментов, приложенных к ротору двигателя:

где





В статике




Условие




Рис. 2.17. К устойчивости работы асинхронного двигателя.
При малейшем изменении момента нагрузки



Этот процесс будет протекать до полной остановки двигателя. При случайном уменьшении статического момента ротор ускоряется, скольжение уменьшается. Момент двигателя вследствие уменьшения скольжения возрастает, что приводит к увеличению разности







Это условие выполняется для всех практически встречающихся механизмов, если двигатель работает на участке OM механической характеристики. Следовательно, двигатель может работать устойчиво только в диапазоне скольжений ротора



Приведенное выше условие является необходимым, но недостаточным. Когда двигатель работает при скольжении, меньшем



Так как величина момента пропорциональна квадрату питающего напряжения, то даже сравнительно небольшое изменение питающего напряжения может привести к существенному снижению

Характеристиками асинхронного двигателя называются зависимости скорости вращения










Рис. 2.18. Рабочие характеристики асинхронного двигателя.
Скорость вращения ротора


Вращающий момент на валу машины






Момент




Зависимость тока статора асинхронного двигателя от полезной мощности

Зависимость коэффициента полезного действия асинхронного двигателя

Коэффициент мощности асинхронного двигателя


При дальнейшем росте нагрузки

2.3.1. Пуск в ход асинхронных двигателей
Практически используются следующие способы пуска: непосредственное подключение обмотки статора к сети (прямой пуск); понижение напряжения, подводимого к двигателю при пуске; подключение к обмотке ротора пускового реостата.
Прямой пуск применяется для двигателей малой и средней мощности. Обычно при прямом пуске действующее значение пускового тока превосходит номинальное значение в четыре – шесть раз, а пусковой момент примерно равен:


Прямой пуск самый распространенный способ пуска в ход асинхронных двигателей. Недостатками его являются: большой пусковой ток и сравнительно малый пусковой момент, достоинство – простота.
Пуск асинхронного двигателя при пониженном напряжении применяют для двигателей большой мощности. Понижение напряжения может осуществляться тремя способами:
а) путем переключения обмотки статора при пуске с нормальной схемы “треугольник” на пусковую схему “звезда”. В этом случае фазовое напряжение уменьшается в


б) путем включения в цепь статора на период пуска добавочных активных или реактивных сопротивлений.
в) путем подключения двигателя к сети через понижающий автотрансформатор. Секции трансформатора в процессе пуска переключаются соответствующей аппаратурой.
Недостатком всех этих способов является значительное уменьшение пускового момента, который пропорционален квадрату приложенного напряжения. Поэтому пуск асинхронного двигателя при пониженном напряжении может применяться только при пуске двигателей без нагрузки.
Пуск с помощью пускового реостата применяется для двигателей с фазовым ротором. Этим способом можно осуществить пуск двигателя при

Автотрансформатор (рис. ) имеет одну обмотку – обмотку высшего напряжения.
Обмотка низшего напряжения является частью обмотки высшего напряжения.


Рис. 1.31. Принципиальная схема автотрансформатора.
Часть обмотки





Полная расчетная мощность остальной части обмотки:

Так как

то

Расчетная мощность трансформатора:

При одной и той же передаваемой мощности:

Чем ближе




Динамические свойства тахогенераторов. Дифференциальное уравнение тахогенератора:

где
Т – постоянная времени;
Ky – статический коэффициент по напряжению;

Решение уравнения (5.5.13):

где

Передаточная функция тахогенератора:

Из этого уравнения, очевидно, что тахогенератор представляет собой инерционное дифференцирующее звено. Постоянная времени Т определяется скоростью протекания электромагнитных процессов в машине, т. е. активными и реактивными сопротивлениями самой машины и ее нагрузки. Электромеханической постоянной времени, обусловленной инерцией полого ротора тахогенератора, обычно пренебрегают.
Литература
1. Костенко М П., Пиотровский Л. М. Электрические машины, Л, “Энергия”, 1973.
2. Вольдек А. И. Электрические машины, Л, “Энергия”, 1974.
3. Брускин Д. Э., Зорохович А. Е., Хвостов В. С. Электрические машины и микромашины, М, “Высшая школа”, 1990.
4. Пиотровский Л. М. Электрические машины, Л, “Госэнергоиздат ”, 1963.
5. Арменский Е. В., Прокофьев П.А., Фалк Г. Б. Автоматизириванный электропривод, М, “Высшая школа”, 1987.
Оглавление
1. Расчет магнитный цепей (общие сведения). . . . . . . . . . . . . . . . . . . . . . . . . . 2

Холостой ход трансформатора
При холостом ходе трансформатора имеем

Первое из уравнений ничем не отличается от уравнения катушки с ферромагнитным сердечником. Следовательно, векторная диаграмма трансформатора (рис.1.18) в режиме холостого хода будет аналогичной векторной диаграмме катушки.

Рис.1.18.Векторная диаграмма трансформатора в режиме х.х.
Следует иметь ввиду, что на векторной диаграмме не отображены количественные соотношения между напряжениями I10R1, I10xр1 и ЭДС E1 и E2. На самом деле, напряжения I10R1, I10xр1 составляют всего несколько процентов E1. В свою очередь ток холостого хода I10 составляет всего от 10 до 4% номинального тока трансформатора. Поэтому с помощью опыта холостого хода определяется коэффициент трансформации:

Этот коэффициент указывается на щитках трансформаторов как отношение высшего напряжения к низшему:

Мощность потерь в обмотках трансформатора в режиме холостого хода пренебрежимо мала, так как ток I10 достаточно мал. Все потери в этом режиме работы трансформатора определяются потерями в сердечнике.
Исполнительный двигатель с фазовым управлением
Напряжения прямой и обратной последовательностей (как было показано выше):


Рассмотрим работу идеализированного двигателя с фазовым управлением при упрощающем предположении






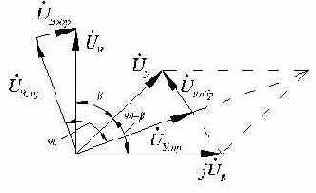
Рис. 2. 30. Векторная диаграмма напряжений управления и возбуждения при фазовом управлении асинхронного двухфазного двигателя.
модуль напряжения прямой последовательности

а обратной последовательности

Так как в данном случае полные сопротивления соответствующих схем замещения равны


то выражения для токов принимают вид:

Если пренебречь всеми сопротивлениями обмоток, кроме активного сопротивления, то полные сопротивления схемы замещения

В этом случае выражения для токов прямой и обратной последовательностей принимают вид:

Измерительные трансформаторы
Измерительные трансформаторы применяются для изоляции измерительных приборов от высокого напряжения и расширения пределов измерения вольтметров и амперметров (рис.1.32).

Рис.1.32. Схема включения измерительного трансформатора напряжения.
Измерительные трансформаторы делятся на трансформаторы напряжения и трансформаторы тока. Соединение обмоток по группе 12.
Вторичное номинальное напряжение у всех трансформаторов напряжения согласно ГОСТ равно 100 В.
До 6 кВ трансформаторы напряжения изготавливаются сухими, т.е. с естественным охлаждением. Свыше 6 кВ трансформаторы напряжения изготавливаются жидкостными.
Измерительные приборы, работающие с измерительными трансформаторами, градуируются с учетом коэффициента трансформации

Трансформатор тока со стороны первичной обмотки включается как амперметр (рис. 1.33а).
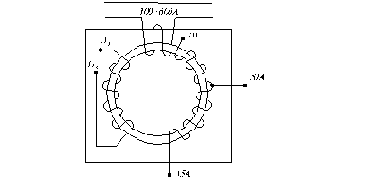

а) б)
Рис. 1.33. Схема включения измерительного трансформатора тока (а)
и его устройство (б).


При большой величине сопротивления в измерительной цепи нарушается это приближенное равенство и точность показаний прибора, обмотка которого питается от измерительной цепи трансформатора тока, ухудшается.
Чем меньше магнитное сопротивление магнитной цепи, тем меньше (согласно закону Ома для магнитной цепи) должен быть ток намагничивания




Нельзя размыкать измерительную цепь трансформатора тока, т. к. ток намагничивания

Показания ваттметра необходимо умножить на два коэффициента:



Эквивалентная схема и параметры приведенного трансформатора
При расчетах необходимо сопоставить параметры первичной и вторичной цепей трансформатора. Если коэффициент трансформации велик, например, более 100, то изобразить векторные диаграммы первичной и вторичной цепей невозможно, т. к. при конкретных величинах векторов напряжении, токов и падений напряжений первичной (вторичной) цепи векторная диаграмма вторичной (цепи) вырождаются в точку. Эту проблему можно решить, если пользоваться приведенной схемой замещения трансформатора, в которой число витков вторичной обмотки равно числу витков первичной, но при этом не изменяются энергетические соотношения. Положим, что вторичная обмотка приводится к первичной, тогда







Эквивалентную схему замещения
Рис.1.20. Схема замещения трансформатора с учетом потерь в магнитопроводе.



Рис.1.21. Схема замещения приведенного трансформатора с учетом потерь в магнитопроводе.
Эллиптическое поле
Круговое вращающееся магнитное поле возникает только при симметрии токов, проходящих по катушкам (симметрии НС катушек отдельных фаз), при симметричном расположении этих катушек в пространстве и при сдвиге во времени между фазовыми токами, равном пространственному сдвигу между катушками. При несоблюдении хотя бы одного из этих условий возникает не круговое, а эллиптическое вращающееся поле (рис.2.22а), у которого максимальное значение результирующей индукции для различных моментов времени не остается постоянным, как при круговом поле. В таком поле пространственный вектор НС



Рис. 2.22. Эллиптическое магнитное поле в рабочем зазоре машины (а) и его разложение на два составляющих круговых поля: прямое (б) и обратное (в).
двух эквивалентных круговых полей, вращающихся в противоположных направлениях рис.2.22б, в). Разложение эллиптического поля на прямое и обратное круговые поля производится методом симметричных составляющих, с помощью которого определяются НС прямой и обратной последовательностей. Рассмотрим, как осуществляется это разложение на примере двухфазной обмотки при питании ее несимметричными токами.
Допустим, что НС




причем в общем случае

Представим каждый из векторов НС






При этом


Векторы







|
|
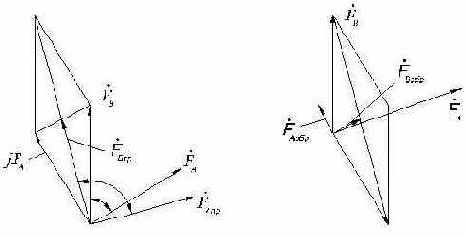
Рис. 2.23. Диаграмма разложения векторов НС двухфазной обмотки на систему векторов прямой (а) и обратной (б) последовательностей.
образуют систему векторов НС обратной последовательности (рис. 2.23б), причем вектор



Величины векторов прямой и обратной последовательностей найдем, подставив последнюю систему в выражения для



Умножим первое уравнение системы на


Получаем


Так как

то уравнения бегущей волны для прямого и обратного круговых полей имеют вид:

При рассмотрении работы многофазных электрических машин, обычно заданными величинами являются напряжения, подводимые к машине, и сопротивления фаз. В общем случае для определения свойств машины требуется разложить на симметричные составляющие подводимые напряжения, по которым затем определяются токи и НС прямой и обратной последовательностей.
Перейдем от системы НС (2.34) к системе токов:

где


Так как

то

где

В каждой из фаз токи прямой и обратной последовательностей создают падения напряжений, сумма которых равна подведенному напряжению:

где

С учетом выражений



Круговое вращающееся магнитное поле
Если на статоре электрической машины разместить трехфазную обмотку, у которой оси фаз (A-X, B-Y, C-Z) сдвинуты в пространстве на

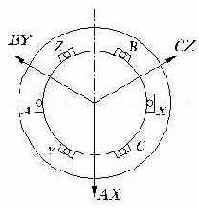
Рис. 2.21. Расположение фазных обмоток на статоре двухполюсной трехфазной машины.
то при питании ее симметричным трехфазным током получим круговое вращающееся магнитное поле. На рис.2.21 фазовые обмотки для простоты показаны сосредоточенными, но распределение НС, образуемое каждой обмоткой, следует считать синусоидальным. Ввиду того, что в рассматриваемой обмотке фазы A-X, B-Y и C-Z смещены в пространстве на (









Результирующую НС в точке x можно получить сложив отдельные составляющие


Полученное уравнение бегущей волны позволяет в любой момент времени t найти точку x, в которой НС максимальна и равна








она совершит 1/p оборота вокруг оси машины.
Очевидно, что:
За (pT) секунд бегущая волна совершит 1 полный оборот вокруг оси машины, а
за 1минуту (60 секунд) – n оборотов.
Приведенная пропорция позволяет найти выражения для скорости вращения магнитного поля в рабочем зазоре машины


В общем случае, когда по симметричной т-фазной обмотке, фазы которой сдвинуты в пространстве на угол



Так, например, в двухфазной обмотке с фазами, смещенными в пространстве на половину полюсного деления, создается круговое вращающееся магнитное поле, если по ее фазам протекают симметричные токи, сдвинутые во времени на угол


Круговое вращающееся магнитное поле обладает следующими свойствами:
а) максимум результирующих волн НС и индукции всегда совпадают с осью той фазы, в которой ток имеет максимум. Это положение легко проверить, задаваясь величиной


б) магнитное поле перемещается в сторону оси той фазы, в которой ожидается ближайший максимум. Это свойство непосредственно следует из предыдущего;
в) для изменения направления вращения поля необходимо изменить порядок чередования тока в фазовых обмотках. В трехфазных машинах для этой цели следует поменять местами провода, подводящие ток из трехфазной сети к двум любым фазам обмотки; в двухфазных - переключить провода, присоединяющие две фазы обмотки сети.
Магнитная цепь с переменной магнитодвижущей силой (МДС)
На рис. 1.7а показана схема подключения катушки с ферромагнитным сердечником к источнику синусоидального напряжения.
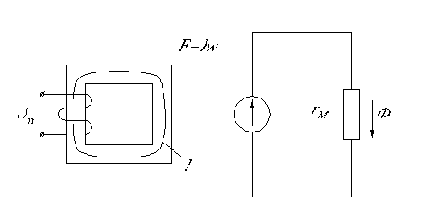



а)
б)

Рис.1.7. Катушка с ферромагнитным сердечником, схема замещения ее магнитной цепи (а), зависимость магнитного потока и индуктивности катушки от тока (б).
Рассмотрим электромагнитные процессы в цепи катушки с ферромагнитным сердечником при подключении ее к синусоидальному напряжению (рис.1.8).

Рис.1.8. Схема замещения электрической цепи катушки с ферромагнитным сердечником.
На основании второго закона Кирхгофа имеем:

Активное падение напряжения ir относительно мало и для анализа общего характера процесса им можно пренебречь:

отсюда
Ф= -

Здесь A – постоянная величина магнитного потока, которая при питании синусоидальным напряжением (в установившемся режиме) равна нулю. Поэтому

где

Будем считать, что начальная фаза потока равна 0, т.е.








- уравнение трансформаторной ЭДС.
Связь между магнитным потоком и возбуждающим его током отображается петлей гистерезиса.

Рис.1.9. Построение кривой тока катушки с ферромагнитным сердечником.
Используя синусоидальную кривую потока и частный цикл гистерезиса, построим зависимость i(t) (рис.1.9). Анализ этой кривой показывает, что гистерезисная петля приводит к появлению угла сдвига фаз между потоком и вызывающим его током. Насыщение сердечника приводит к появлению пика в кривой тока. Чем больше величина магнитной индукции в сердечнике, тем больше и острее этот пик, что говорит о несинусоидальности кривой тока.
Заменим несинусоидальный ток эквивалентным синусоидальным. Условием эквивалентности является равенство действующих значений этих токов и равенство потерь, которые они вызывают. Эта замена позволит использовать методы расчетов цепей синусоидального тока и построить векторную диаграмму для катушки с ферромагнитным сердечником. Так как между несинусоидальным током и потоком существует сдвиг фаз, то и эквивалентный синусоидальный ток опережает поток на угол


Рис.1.10. Векторные диаграммы магнитного потока, ЭДС и тока катушки с ферромагнитным сердечником.
Величина угла

Рассмотрим распределение магнитного потока в ферромагнитном сердечнике катушки (рис.1.11).

Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником
Хотя магнитная проницаемость сердечника в несколько тысяч раз больше магнитной проницаемости воздуха, часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Фр (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

Так как


То есть поток рассеяния





Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником.
Будем считать, что все витки обмотки катушки с ферромагнитным сердечником сцеплены с Фр, тогда

Lр=









Величина



U=-e+ri-eр= -e+ri+Lр

В комплексной форме



где
Z= r+jxр; xр=

На рис.1.13 построена векторная диаграмма катушки с ферромагнитным сердечником.

Рис.1.13 Полная векторная диаграмма катушки с ферромагнитным сердечником.
Разложим вектор тока катушки




Используя векторную диаграмму, получим эквивалентную схему замещения катушки с ферромагнитным сердечником (рис.1.14).

Рис.1.14. Схема замещения катушки с ферромагнитным сердечником.
Из уравнения трансформаторной ЭДС (1.13) определяем число витков катушки:
w=



Ток намагничивания определяется по формуле:
Iф=

Ток потерь в сердечнике:
In

Полный намагничивающий ток катушки:
I=

Приведем выражения, позволяющие рассчитать потери в сердечнике от гистерезиса и от вихревых токов. Потери в сердечнике от гистерезиса пропорциональны площади петли гистерезиса. Следует иметь ввиду, что ширина петли гистерезиса растет с увеличением частоты.

где

f – частота;
G – вес сердечника;
n=1,6 при Bm<1Тл и n=2 при Bm>1Тл.
Под действием переменного магнитного потока в сердечнике возникают вихревые токи (рис. 1.15).

Рис.1.15. К эффекту возникновения вихревых токов в ферромагнитном сердечнике.
Пусть вектор магнитного потока направлен, как показано на рис.1.15. Тогда в сердечнике, в плоскости перпендикулярной потоку возникнет ЭДС, под действием которой возникнут вихревые токи. Направление ЭДС таково, что создаваемый ими поток уменьшает вызвавший ЭДС поток

Потери на вихревые токи

где


1.5. Трансформаторы
Трансформатором называется статический электромагнитный аппарат, передающий энергию из одной цепи в другую посредством электромагнитной индукции. Он применяется для различных целей, но чаще всего служит для преобразования напряжения и тока.
Трансформаторы бывают: силовые, измерительные, специального назначения. Кроме того, трансформаторы различаются по числу фаз на однофазные и трехфазные; по способу охлаждения на сухие и жидкостные.
Условные обозначения трансформаторов (рис 1.16):
|
|
|
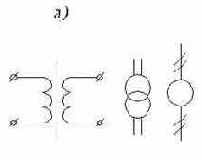
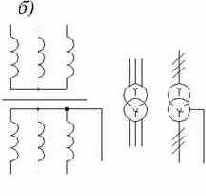
Машины переменного тока
Принцип действия машин переменного тока (синхронных и асинхронных) обусловлен взаимодействием вращающегося магнитного поля, создаваемого обмотками статора, с током ротора. Поэтому, прежде чем приступить к анализу электромагнитных процессов в машинах переменного тока, рассмотрим, как образуется вращающееся магнитное поле.
Механическая мощность
Механическая мощность двигателя в относительных единицах

При заданном коэффициенте сигнала максимум механической мощности имеет место при скорости


или

отсюда

Следовательно, максимальную мощность двигатель развивает при скорости, равной половине скорости холостого хода. Подставляя



Очевидно, что при скорости, равной нулю, и при холостом ходе механическая мощность равна нулю. На рис.2.28б показаны изменения механической мощности


Механические характеристики
Электромагнитные мощности для полей прямой и обратной последовательностей:


Мощность поля обратной последовательности создает тормозной момент, следовательно, она является отрицательной. Поэтому результирующая мощность двигателя:

Вращающий момент двигателя

Выразим момент в относительных единицах, приняв за базовую величину значение момента




то относительный момент

откуда

По этой формуле строится механическая характеристика исполнительного двигателя в относительных единицах

|
|

Рис.2.27. Механические (а) и регулировочные (б) характеристики идеализированного двигателя с амплитудным управлением.
С уменьшением




Снижение скорости холостого хода при меньших значениях

Так как в двигателе с полым немагнитным ротором основной составляющей тока статора является ток холостого хода, то ток статора с изменением режима работы двигателя изменяется мало. Мало изменяется и мощность возбуждения, увеличиваясь на 10 – 20% при переходе от режима короткого замыкания к холостому ходу. Мощность управления при амплитудно-фазовом управлении, как и при амплитудном управлении, пропорциональна коэффициенту сигнала и сравнительно мало зависит от скорости вращения. Все другие характеристики (механическая мощность, КПД и др.) при амплитудно-фазовом управлении мало отличаются от характеристик двигателя при амплитудном управлении.
Достоинством амплитудно-фазового управления является сравнительная простота схемы и возможность получения значительных пусковых моментов, недостатком – некоторое снижение устойчивости в зоне малых скоростей.
2.4.9. Электромеханическая постоянная времени исполнительных двигателей
Время разгона исполнительного двигателя определяется, главным образом, электромеханическими переходными процессами, т. к. из-за значительного активного сопротивления электромагнитные переходные процессы в них быстротечны. Электромеханическая постоянная времени





принимает вид

где

Обычно электромеханическую постоянную времени определяют исходя из пускового момента


где

Следовательно, можно записать

или

Решив это уравнение, получим

где

времени:



Физически электромеханическая постоянная времени представляет собой время, необходимое для разгона двигателя от неподвижного состояния до достижения скорости холостого хода при постоянном моменте на валу




В двигателе с амплитудным управлением

где


Поэтому

Из этого выражения следует, что при амплитудном управлении постоянная времени растет с уменьшением эффективного коэффициента сигнала, т. к. уменьшается величина пускового момента. При фазовом управлении



Следовательно, при этом способе управления постоянная времени





Естественно, что время разгона двигателя с уменьшением коэффициента сигнала растет.
Из выражений для постоянной времени







Механические и регулировочные характеристики идеализированного двигателя
Электромагнитная мощность с учетом выражения для



Следовательно, электромагнитный момент

Принимая за базовую величину момент






Рис.2.31. Механические (а) и регулировочные (б) характеристики идеализированного двухфазного асинхронного двигателя при фазовом управлении.
Механические характеристики (рис.2.31а) прямолинейны и параллельны. Наклон их при малых коэффициентах сигналов меньше, чем при амплитудном управлении (пунктирные линии). Это объясняется тем, что при одном и том же коэффициенте сигнала

Данное обстоятельство является существенным преимуществом фазового управления. Особенно ярко это преимущество проявляется при сравнении регулировочных характеристик. Как следует из выражения для

Характеристики реального двигателя при фазовом управлении нелинейны, а скорость холостого хода при

Механические усилия в магнитном поле
На проводник с током I, помещенный в магнитное поле индукции B, воздействует сила, направление которой определяется правилом левой руки (если вектор


где


а)
б)
Рис.1.5. К определению направления действия механической силы в магнитном поле (а) и картины распределения магнитных силовых линий в поле проводника с током(б).

Рис.1.6. К определению силы тяги электромагнита.
Сила тяги электромагнита (рис.1.6) определяется выражением
F=


Мощность управления
Фазовое управление применяется сравнительно редко из-за большой мощности управления при малом коэффициенте сигнала.
Так при неподвижном роторе полная мощность обмотки управления

т. е. не зависит от коэффициента сигнала, т. к. амплитудное значение напряжения управления остается неизменным, а обмотки управления и возбуждения электромагнитно не связаны. Другим недостатком фазового управления является сложность регулирования фазы управляющего сигнала.
2.4.8. Исполнительный двигатель с амплитудно-фазовым управлением (конденсаторная схема)

Рис.2.32. Схема исполнительного двигателя при амплитудно-фазовом управлении (а) и его векторная диаграмма при круговом вращающемся поле (б).
Напряжение управления






Так как при изменении напряжения управления или скорости вращения двигателя изменяется величина тока


Если подобрать коэффициент сигнала



Подставив сюда значения токов в фазах управления и возбуждения


где:




или

Отсюда


Условия, необходимые для создания кругового поля


Величина емкости




где индекс “k” означает, что сопротивления


Мощности управления и возбуждения
Ток идеализированного двигателя является чисто активным, поэтому мощности обмоток управления и возбуждения будут определяться следующим образом:

Ток управления с учетом выражений для



Мощность управления:

Аналогично, ток возбуждения:

(т. к.


и мощность в обмотке возбуждения:

При круговом вращающемся поле и неподвижном роторе:

т. е. вся мощность






Рис.2.28. Зависимости мощностей управления и возбуждения (а) и механической
мощности (б) идеализированного двигателя с амплитудным управлением от относительной частоты вращения.

Графики зависимости относительных мощностей


а) мощность обмотки управления резко падает с уменьшением коэффициента сигнала так, что с точки зрения уменьшения мощности управления выгодно работать при малых коэффициентах сигнала;
б) при пуске мощность обмотки возбуждения не зависит от коэффициента сигнала. Объясняется это тем, что при неподвижном роторе обмотки управления и возбуждения электромагнитно не связаны между собой и не могут влиять друг на друга.
Основные соотношения для однофазного трансформатора

Трансформатор состоит из двух или более обмоток, расположенных на общем сердечнике, который для улучшения магнитной связи между обмотками изготавливается из ферромагнитного материала (рис. 1.17а).
а) б)
Рис.1.17. Устройство однофазного трансформатора (а) и его схема замещения (б).
При анализе электромагнитных процессов в катушке с сердечником мы выяснили, что при питании ее синусоидальным напряжением магнитный поток можно считать синусоидальным, несмотря на нелинейность зависимости B=f(H):
Ф=Фmsin

Этот поток сцеплен с двумя обмотками w1 и w2 и индуцирует в них ЭДС:


E1=4,44w1fФm; E2=4,44w2fФm..
Из последних двух выражений

Величина

При номинальной нагрузке КПД трансформатора достигает 98%. Это дает возможность считать одинаковыми первичную и вторичную полные мощности трансформатора:
S1=U1I1

Тогда

Как и в цепи катушки с ферромагнитным сердечником, заменим несинусоидальный ток трансформатора эквивалентным синусоидальным и, учитывая индуктивности рассеивания первичной обмотки Lр1 и вторичной обмотки Lр2:
xр1=


а также
R1 – активное сопротивление первичной обмотки;
R2 – активное сопротивление вторичной обмотки;
Zн – сопротивление нагрузки,
запишем уравнения для обеих цепей по 2-му закону Кирхгофа в комплексной форме (рис. 1.17б):

Основные технические показатели
Мст = (2…10)10-4 Нм (2…10 Гсм).
Максимальная рабочая скорость nmax достигает 8000…10000 об/мин; относительная скорость

Особенности работы трехфазных трансформаторов
Все соотношения, которые мы получили для однофазных трансформаторов, справедливы и для трехфазных трансформаторов, точнее для одной фазы трансформатора, нагруженного симметрично.
Возьмем три однофазных трансформатора и подключим их к трехфазной цепи (рис.1.26).
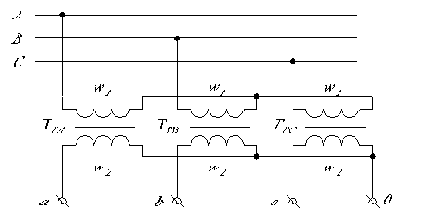
Рис.1.26. Трехфазный трансформатор, состоящий из трех однофазных.
В результате на выводах a,b и c получим три фазных напряжения (по отношению к выводу 0)



а) б)
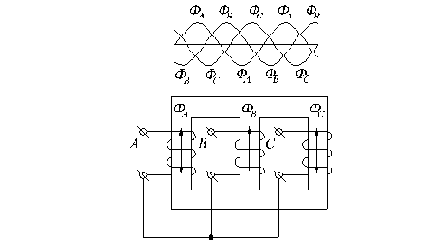

Рис.1.27. Устройство трехфазного трансформатора (а) и его схема замещения магнитной цепи (б).
На каждый из стержней магнитопровода наматывается одна первичная обмотка и одна или несколько вторичных обмоток трансформатора. Магнитное сопротивление



Обмотки трансформатора соединяются звездой (Y) или треугольником (


Отношение


Согласно закону Ленца ток



Рис.1.28. Соединение трехфазного трансформатора по схеме: Y/


Рис.1.29. К определению направления тока во вторичной обмотке трансформатора.
Все многообразие способов соединений согласно ГОСТ делится на 12 групп. При определении номера группы (рис.1.30) минутная стрелка часов устанавливается на цифре 12 и с ней совмещается вектор линейного высшего напряжения, а часовая стрелка
совмещается с вектором линейного низшего напряжения. Отсчет угла производится от минутной стрелки к часовой по направлению их вращения.
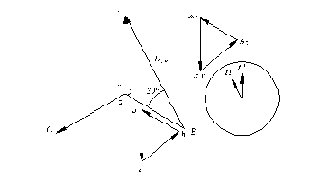
группа11
Рис.1.30. К определению номера группы трансформатора.
Получение кругового вращающегося магнитного поля
Круговым вращающимся магнитным полем называется поле, вектор результирующей магнитной индукции которого неизменен и вращается с постоянной угловой скоростью. Рассмотрим, как изменяется магнитное поле катушки, по которой протекает переменный ток (рис. 2.1):


Рис. 2.1. К определению направления вектора НС катушки с переменным током.
Из рис. 2.1 видно, что вектор магнитной индукции





Рис. 2.2. К получению кругового вращающегося магнитного поля в двухфазной электрической цепи.
Если оси двух катушек




то векторы магнитной индукции катушек сдвинуты относительно друг друга также на 90 электрических градусов.
Так как обе катушки совмещены в пространстве, то они создают магнитное поле, модуль вектора результирующей магнитной индукции которого будет равен

Рис. 2.3. К расчету модуля вектора результирующей магнитной индукции.


отсюда

За один период изменения тока двухфазной питающей сети вектор результирующей магнитной индукции сделает один полный оборот:

За одну секунду результирующий вектор магнитной индукции делает



Вращающееся магнитное поле является круговым при соблюдении следующих условий: сдвиг катушек в пространстве на угол


Нарушение любого из условий образования кругового вращающегося магнитного поля приводит к образованию эллиптического поля, при котором конец вектора результирующей магнитной индукции описывает не окружность, а эллипс (рис.2.4). В этом случае вектор результирующей магнитной индукции изменяется по амплитуде.
Эллиптическое поле можно представить как сумму двух неравных по амплитуде круговых полей, вращающихся с синхронной частотой


Рис.2.4. Образование эллиптического вращающегося магнитного поля.
Круговое поле


Прямое поле создает вращающий момент двигателя













При неподвижном роторе оба поля вращаются относительно ротора с одинаковой частотой и скольжением. Каждое из них наводит в обмотке ротора токи, равные по амплитуде вследствие равенства полей и скольжений. Возникают равные по модулю вращающие моменты


Таким образом, изменяя форму поля от пульсирующего через эллиптическое до кругового, можно регулировать вращающий момент от нуля при пульсирующем поле до максимального при круговом.
Соответственно частота вращения ротора будет изменяться от нуля при пульсирующем поле до максимальной при круговом. Способ управления, основанный на изменении амплитуды напряжения управления





Рассмотрим теперь получение кругового вращающегося магнитного поля в трехфазной электрической цепи.
Возьмем три одинаковые катушки с токами:


Рис.2.5. К образованию кругового вращающегося магнитного поля в трехфазной цепи.







Рис.2.6. Вращение вектора результирующей магнитной индукции

Вектор результирующей магнитной индукции равен




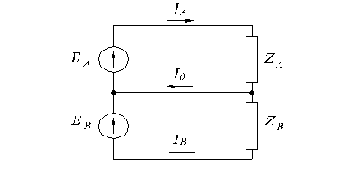
а)



б)

Рис.2.7. Распределение токов в двухфазной (а) и трехфазной (б) электрических цепях.
При симметричной нагрузке



2.2. Основные принципы выполнения многофазных обмоток
В электрических машинах переменного тока обмотки размещаются в пазах, расположенных на внутренней поверхности статора и внешней поверхности ротора электрической машины. Проводники обмотки соединяются между собой, образуя ряд катушек. Все катушки одной группы соединяются между собой, образуя одну фазу обмотки. Каждая из фаз обмотки может иметь несколько параллельных ветвей.
Каждый виток обмотки размещается в пазах, находящихся друг от друга на расстоянии, примерно равном одному полюсному делению


где
D – диаметр внутренней расточки статора;
p – число пар полюсов.
Если под каждым полюсом расположено только по одной катушке каждой фазы, то такая обмотка называется сосредоточенной. При большем числе катушек под каждым полюсом обмотка называется распределенной.
а) б)

Рис.2.8. Схема двухполюсной машины с сосредоточенной обмоткой (а) и диаграмма распределения ее намагничивающей силы (б).
Намагничивающая сила, создаваемая обмоткой переменного тока, распределена вдоль окружности статора и ротора. Форма кривой ее распределения зависит от типа обмотки. Обычно стремятся, чтобы эта кривая была по возможности близка к синусоиде. При этом ЭДС, индуктируемые в катушках, образующих обмотку статора, будут иметь приблизительно синусоидальную форму, т. е. высшие гармоники в кривой ЭДС будут малы.
Для этой цели принимают ряд мер: распределение каждой фазы по нескольким пазам, укорочение шага обмотки и скос пазов.
Рассмотрим сначала двухполюсную машину с простейшей сосредоточенной обмоткой, у которой все витки, включенные в фазу

При максимальном значении тока в катушке намагничивающая сила


При питании переменным током однофазной обмотки возникает магнитное поле, пульсирующее во времени с частотой

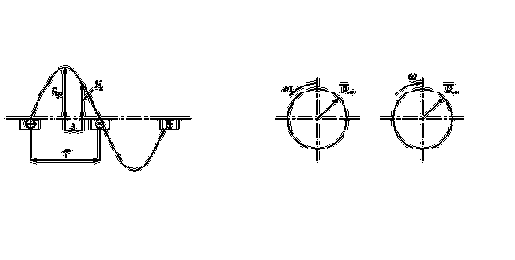

где

|
|
|
Рис.2.9.Диаграмма распределения намагничивающей силы в воздушном зазоре (а) и годографы пространственного вектора МДС (б, в).
Это выражение можно преобразовать к виду:

Каждый из членов полученного выражения представляет собой вращающуюся или бегущую волну намагничивающей силы. В данном случае образуются две, вращающиеся в противоположные стороны волны НС: прямая волна


Продольная составляющая НС ротора

где
E1m – действующее значение ЭДС в выходной обмотке в случае, когда вектор НС совпадает с осью этой обмотки.
Обычно удобнее иметь при согласованном положении приемника и датчика нулевой сигнал. Поэтому ротор и статор сельсина приемника при согласованном положении ведущей и ведомой осей предварительно смещают на 900 относительно ротора или статора сельсина – датчика. В этом случае выходной сигнал изменяется по закону

При выборе сельсина, предназначенного для трансформаторного режима работы, важно знать величину удельного выходного напряжения, т.е. величину Uвых, приходящую на 10 угла рассогласования:

Эта величина обычно приводится в паспорте сельсина. Для того, чтобы зависимость выходного сигнала Uвых от угла рассогласования

Индикаторные режимы работы однофазных сельсинов. В этом режиме на валу сельсина – приемника имеется незначительный момент сопротивления, поэтому для поворота ротора приемника вслед за поворотом ротора датчика требуется небольшой вращающий момент, который может быть получен от самого сельсина – приемника без дополнительных усилительных устройств.
Схема включения сельсинов для индикаторного режима имеет вид (рис. 5.11):

Рис. 5.11. Схема включения сельсинов при работе их в индикаторном режиме.
Пульсирующие магнитные потоки, создаваемые обмотками возбуждения датчика и приемника, индуктируют в трех фазах обмоток синхронизации ЭДС. Если между роторами датчика и приемника имеется некоторый угол рассогласования

Эти моменты имеют противоположные направления и стремятся свести к нулю угол рассогласования. Обычно ротор датчика заторможен, поэтому его синхронизирующий момент воспринимается механизмом, поворачивающим ведущую ось О1; синхронизирующий же момент приемника поворачивает его ротор в ту же сторону и на тот же угол, на который поворачивается ротор датчика.
В трех фазах обмотки синхронизации датчика потока возбуждения Фв индуцирует ЭДС:

Так как обмотка возбуждения приемника присоединена к той же сети однофазного тока, то в фазах его обмотки синхронизации будет индуцироваться ЭДС:

В виду того, что ЭДС в одноименных фазах датчика и приемника направлены по контуру, образованному проводами линии связи, встречно, токи в фазах датчика и приемника:

Представим ток в фазах обмоток синхронизации в виде двух составляющих:

где составляющая со «штрихом» обусловлены наличием ЭДС EД в обмотках датчика, а «два штриха» – ЭДС En в обмотках приемника. Это позволяет при определение НС в датчике и приемнике воспользоваться результатами, полученными для дифференциального режима работы сельсинов.
Составляющие токов



направленную по продольной оси, а в приемнике НС-

продольная и поперечная составляющие которой равны

Составляющие же токов



направленную по продольной оси, а в датчике НС


.

Рис. 5.12. Составляющие векторов НС ротора FД и FП в датчике (а) и в приемнике (б), обусловленные действием ЭДС ЕД и ЕП.
При этом результирующие НС (рис. 5.12) будeт иметь следующие составляющие:
В датчике

в приемнике

При

При наличии угла рассогласования появляются токи и НС ротора, величины которых в датчике и приемнике одинаковы:


Рис. 5.13. Положение векторов НС ротора FД и FП в датчике (а) и в приемнике (б) при повороте ротора датчика на угол

На рис. 5.13 показаны токи и НС датчика и приемника при угле рассогласования датчика




Продольные составляющие FДd и Fnd НС ротора датчика и приемника создают в обеих обмотках возбуждения компенсационные токи (аналогично трансформатору), НС которых компенсирует действие НС FДd и Fnd. Поперечные же составляющие FДq и Fnq, оставшиеся нескомпенсированными, взаимодействуют с потоком статора, создавая в датчике и приемнике синхронизирующие моменты.
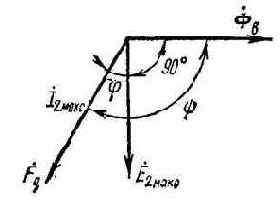
Рис. 5.14. Векторная диаграмма для ротора сельсина-приемника.
Векторная диаграмма для ротора сельсина (рис. 5.14) подобна векторной диаграмме для ротора асинхронного двигателя. Поперечная составляющая



Величину и направление синхронизирующего момента можно определить также, как и в обычной асинхронной машине, считая, что момент создается активной составляющей ротора. Это наглядно показано на рис. 5.15,

Рис. 5.15. Схема возникновения синхронизирующего момента в датчике (а) и в приемнике (б).
где крестиками и точками показано направление составляющих тока ротора, соответствующих некомпенсированным поперечным НС FДq и Fnq. Из рис. 5.15 следует, что синхронизирующие моменты в датчике и приемнике направлены в противоположные стороны и стремятся повернуть оба ротора в согласованное положение. На ротор датчика действует момент Мc.Д., стремящийся возвратить ротор в исходное положение, а на ротор приемника - момент Мc.n, увлекающий его в сторону поворота ротора датчика.
Мгновенное значение синхронизирующего момента:

где С и С1 – постоянные.
Следовательно, при заданном угле рассогласования

Среднее значение синхронизирующего момента:

Принимая sinj=const и обозначая


Таким образом, средняя величина синхронизирующего момента пропорциональна синусу угла рассогласования. Для того, чтобы сельсины обладали свойством самосинхронизации в пределах одного оборота, их обычно выполняют двухполюсными так, что геометрический угол поворота ротора

Из рис. 5.16а, следует, что синхронизирующий момент равен нулю при углах рассогласования






Рис. 5.16. Зависимости синхронизирующего момента от угла рассогласования в сельсинах с неявновыраженными (а) и явновыраженными (б) полюсами
Величина максимального синхронизирующего момента Mm зависит от произведения
F2m sinj. Так как



где
A и B – постоянные;
UB – напряжение, подаваемое на обмотку возбуждения сельсинов.
Z2,r2 и x2 – суммарное, активное и индуктивное сопротивления последовательно включенных фаз датчика и приемника (для сельсинов с явновыраженными полюсами (рис. 5.16б) берут значения Z2 и x2 приведенные к поперечной оси сельсина).
Взяв производную момента Mm по x2 и прировняв её нулю, можно определить значение x2, при котором этот момент имеет наибольшую величину:

отсюда x2= r2.
Таким образом, для получения наибольшей величины Mm необходимо иметь равные индуктивное и активное сопротивления ротора сельсина.
Важной характеристикой сельсина является удельный синхронизирующий момент (момент, приходящийся на 10 угла рассогласования).

Часто этим термином обозначают также крутизну S нарастания синхронизирующего момента в начальной части характеристики M=¦(


Момент





Для увеличения удельного синхронизирующего момента при малых углах рассогласования сельсины, предназначенные для работы в индикаторном режиме, выполняются, как правило, с сосредоточенной обмоткой возбуждения и явно выраженными полюсами на статоре.
Благодаря этому появляется дополнительный реактивный момент Мр, который усиливает результирующий удельный синхронизирующий момент примерно на 10..20 %.
Возникновение реактивного момента можно объяснить притяжением ротора, являющегося электромагнитом, к выступающим полюсам статора (рис. 5.17).
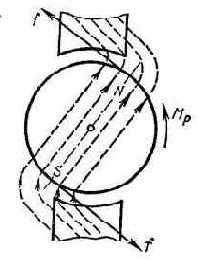
Рис. 5.17. Схема возникновения реактивного момента.
Погрешность в сельсинах. Погрешность при работе сельсинов в индикаторном и трансформаторном режимах вызываются электрической, магнитной и механической асимметрией датчика и приемника, обусловленными технологическими причинами, влиянием высших гармоник в кривой НС ротора, влиянием сопротивления линии связи, изменением напряжения питающей сети и др. Кроме того, при работе сельсинов в трансформаторном режиме погрешность в работе сельсинов может быть вызвана тормозным моментом на валу приемника.
Устранить технологические погрешности можно, обеспечив высокую точность штамповки листов ротора и статора и сборки их пакетов, строгую концентричность цилиндрических поверхностей ротора и статора (равномерность воздушного зазора, тщательную балансировку ротора и пр.). Уменьшить высшие гармоники в кривой НС ротора можно применением синусных (точных) обмоток. При работе сельсинов в трансформаторном режиме весьма важно, чтобы при

В тех случаях, когда датчик удален на значительное расстояние от приемника, сопротивление линии связи становится соизмеримым с собственным сопротивлением обмоток синхронизации. Это приводит к уменьшению тока в обмотках синхронизации датчика и приемника, вследствие чего уменьшается выходное напряжение

Для уменьшения влияния контактов на работу сельсинов и снижения трения в их подвижных частях стремятся по возможности уменьшить число скользящих контактов.
С этой целью обмотку синхронизации, в большинстве случаев, располагают на статоре, а возбуждения – на роторе. Тогда изменение переходного сопротивления контактов мало сказывается на точности работы системы передачи угла; выход их из строя не приводит к полному нарушению работы системы (в этом случае сельсин – приемник работает как синхронный реактивный двигатель). Недостатком сельсинов с обмоткой возбуждения на роторе является то, что ток через скользящие контакты проходит у них постоянно, в то время как у сельсинов с обмоткой возбуждения на статоре контакты пропускают ток только в момент отработки угла. Однако токи возбуждения сельсинов обычно малы, поэтому надежность работы сельсинов с обмоткой возбуждения на роторе будет значительно выше, чем при расположении её на статоре.
Если сельсины работают в индикаторном режиме, то при значительных расстояниях между датчиком и приемником напряжение, подводимые к их обмоткам возбуждения, могут несколько отличаться по величине и фазе. В этом случае даже при согласованном положении роторов датчика и приемника по обмоткам синхронизации будет проходить ток и возникает определенная погрешность. Для её устранения в цепь возбуждения одной из машин включают дополнительное активно-индуктивное сопротивление, с помощью которого выравнивают по величине и фазе напряжения, подводимые к обмотке возбуждения.
При работе сельсинов в трансформаторном режиме выходная обмотка приемника обычно включается на высокоомный вход усилителя. В этом случае ток в обмотке очень мал и можно сказать, что Uвых@Eвых. Однако, если сопротивление нагрузки Zн не очень велико, то ток нагрузки


где
Z1 – сопротивление обмотки статора, то выходное напряжение

Таким образом, с увеличением нагрузки выходное напряжение (при одном и том же угле рассогласования) уменьшается. Кроме того, при большой нагрузке возникает реакция выходной обмотки, приводящая к таким же искажениям зависимости Uвых=¦(

При работе сельсинов в индикаторном режиме тормозной момент на валу приемника создает довольно существенную погрешность. Так как тормозной момент, создаваемый нагрузкой, в рассматриваемом режиме обычно весьма мал; основное влияние на точность передачи угла оказывает трение в подшипниках приемника и трение щеток о контактные кольца. Погрешность, вызванная моментом трения Мтр сельсина – приемника, характеризует его зону нечувствительности D

Величина этой зоны определяется отношением

чем больше величина


Ток в фазе ротора при индивидуальном питании от датчика одного приемника

а при групповом питании нескольких приемников

Так как максимальный синхронизирующий момент пропорционален НС


То есть погрешность каждого приемника будет больше, чем при индивидуальном питании. Чтобы не допустить увеличение погрешности обычно при групповом питании в качестве датчика используют сельсин с уменьшенным сопротивлением, то есть применяют для этой цели сельсин большей мощности.
В режиме непрерывного вращения сельсинов помимо рассмотренных выше трансформаторных ЭДС в фазах обмотки ротора, датчика и приемника возникают ЭДС вращения, которые по мере роста скорости вращения n уменьшают синхронизирующий момент. Величину динамического синхронизирующего момента в режиме вращения


где



Рис. 5.18. Зависимость динамического синхронизирующего момента от относительной скорости

Обычно при




В зависимости от величины допускаемой погрешности сельсины подразделяются на три класса точности (1,2 и 3). При работе сельсинов в индикаторном режиме погрешность датчика значительно меньше, чем у приемника, так как на последнюю погрешность сильно влияет момент трения. При работе в трансформаторном режиме момент трения приемника воспринимается исполнительным двигателем, поэтому погрешность сельсинов в этом режиме меньше, чем в индикаторном.
5.2.1. Сельсины с одной обмоткой синхронизации.
Для индикаторной передачи угла могут быть использованы сельсины с одной обмоткой на роторе, называемые одноосными (рис.5.19).

Рис. 5.19. Схема включения одноосных сельсинов.
Если оси обмоток ротора датчика и приемника образуют с осью обмотки статора углы, равные соответственно



Подставляя значения



2








получаем


Намагничивающая сила, создаваемая обмоткой ротора, будет пропорциональна току I2:

Синхронизирующий момент можно определить, как и в сельсине с трехфазной обмоткой по выражению:

Так как в данном случае поперечные составляющие НС ротора датчика и ротора приемника:

то формулы для синхронизирующих моментов датчика и приемника будут иметь вид:

Из этих выражений следует, что величина синхронизирующего момента сельсина приемника зависит не только от угла рассогласования, но и от положения ротора приемника. При





5.2.2. Дифференциальные сельсины.
Дифференциальный сельсин используется в тех случаях, когда требуется поворачивать ведомую ось О2 на угол, равный сумме или разности углов поворота двух ведущих осей О1 и O1/ (рис. 5.20).

Рис. 5.20. Схема включения дифференциального сельсина.
В этом случае с ведущими осями механически связаны два сельсина – датчика СД1 и СД2, а с ведомой осью – дифференциальный сельсин ДС. Сельсины – датчики выполнены обычным образом, т. е. имеют однофазную обмотку возбуждения и трехфазную обмотку синхронизации. Конструкция же дифференциального сельсина подобна трехфазному асинхронному двигателю: он имеет на статоре и роторе по три распределенных обмотки, оси которых сдвинуты между собой на 1200; обмотка статора присоединена к обмотке синхронизации датчика СД1, а обмотка ротора – к обмотке синхронизации датчика СД2.

Рис. 5.21. Векторы НС ротора (а) и статора (б) в дифференциальном сельсине при повороте роторов датчика.
В рассматриваемой схеме при любых углах поворота
















5.3. Магнесины
Магнесины являются миниатюрными бесконтактными сельсинами и применяются в системах передачи угла при весьма малых моментах сопротивления на валу приемника (индикаторный режим) и малом расстоянии между датчиком и приемником. Статор магнесина выполнен из листового пермаллоя в виде тороида, на котором намотана спиральная обмотка, подключенная к сети переменного тока (рис. 5.22).
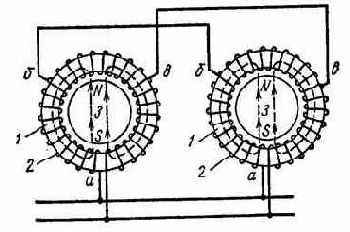
Рис. 5.22. Схема включения магнесина.
Эта обмотка имеет два вывода расположенных под углом 1200 относительно друг друга и относительно точек, к которым подключаются питающие провода. Линия связи ЛС (одним из её каналов является питающая сеть) соединяет одноименные точки а, б и в обмоток статора датчика и приемника.
Ротор магнесина представляет собой постоянный магнит цилиндрической формы, намагниченный по диаметру. При питании обмотки статора переменным током, изменяющимся с частотой ¦1, возникает переменный магнитный поток возбуждения Фв, замыкающийся по тороиду (рис. 5.23).
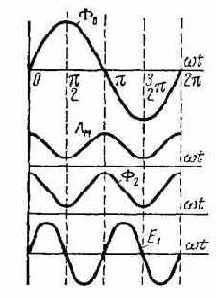
Рис. 5.23. Графики изменения во времени магнитных потоков




Пермаллой, из которого изготовлен тороид, резко изменяет свою магнитную проницаемость при подмагничивании, т. к. он имеет весьма малую коэрцитивную силу (узкую петлю гистерезиса). Поэтому магнитная проводимость


к. поток возбуждения Фв замыкается по тороиду, минуя ротор.
Магнесины, как и сельсины, обладают свойством самосинхронизации в пределах одного оборота, т. к. роторы их поляризованы. Удельный синхронизирующий момент у них небольшой, но из-за малого веса и небольшой инерции ротора магнесины позволяют на небольших расстояниях передавать угол со сравнительно небольшой погрешностью(1-2,50).
5.4. Трехфазные сельсины
В схемах синхронной связи на трехфазных сельсинах в качестве датчика СД и приемника СП используются два обычных асинхронных двигателя с фазными роторами. Их обмотки статора подключаются к общей трехфазной сети переменного тока, а обмотки ротора соединяются друг с другом через контактные кольца (рис. 5.24).

Рис. 5.24. Схема включения трехфазных сельсинов.
При подключении обмоток статора датчика и приемника к сети в сельсинах возникает круговое вращающееся поле, которое индуктирует в одной из фаз ротора датчика ЭДС

а в одноименной фазе ротора приемника – ЭДС

где


приемника.
Знак “+” ставится, если ротор датчика или приемника повернут навстречу вращающемуся полю, а “-”, если он повернут в направлении поля.
При согласованном положении ведущей О1 и ведомой О2 осей, когда углы поворота роторов датчика и приемника равны, ЭДС ЕД и ЕП, индуктированные в одноименных фазах роторов, равны и направлены встречно (рис. 5.25а), вследствие чего по обмоткам роторов ток не протекает. При этом синхронизирующий момент Мс=0.

а) б)
Рис. 5.25. Векторная диаграмма ЭДС и токов для роторной цепи трехфазных сельсинов при отсутствии (а) и при наличии (б) рассогласования.
При появлении угла рассогласования



Этот ток отстает от вектора




При взаимодействии уравнительного тока



где


Если ротор датчика повернут на положительный угол



Характерной особенностью трехфазных сельсинов является то, что синхронизирующие моменты в датчике и приемнике различны, т. к. различны углы



Другим существенным недостатком трехфазных сельсинов является необходимость иметь трехфазный источник питания, поэтому трехфазные сельсины применяются обычно только для синхронного вращения машин большой мощности.
Схема включения трехфазных сельсинов получила название электрического вала (рис.5.26).

Рис. 5.26. Схема электрического вала.
Рабочие механизмы






5.5. Асинхронный тахогенератор
В идеальном случае тахогенератор должен давать на выходе напряжение U, пропорциональное скорости вращения n:


(

Зависимость U= f(n) называется выходной характеристикой.
Тахогенераторы служат для:
- измерения скорости вращения;
- выработки ускоряющих и замедляющих сигналов;
- выполнения операция дифференцирования.
При измерении скорости вращения обычно допустима погрешность 1÷2,5%.
Наибольшая точность требуется в тахогенераторах, работающих в качестве дифференцирующего звена в вычислительных устройствах. В этом случае ошибка в линейности выходной характеристики не должна превышать 0,05÷0,3% по амплитуде. Помимо основного требования к линейной выходной характеристике к ним предъявляются и другие требования: надежность работы в широком диапазоне изменения температуры, влажности, при вибрации и ударных нагрузках; высокое быстродействие; простота устройства; малые размеры и вес; бесшумность и отсутствие радиопомех.
Наиболее полно этим требованиям удовлетворяет асинхронный тахогенератор с полым немагнитным ротором.
Конструкция его аналогична конструкции асинхронного исполнительного двигателя с полым немагнитным ротором (рис. 5.27).
Пульсирующее поле
|
|


Рис. 2.20. Диаграмма распределения НС в воздушном зазоре (а) и годографы пространственного вектора НС прямого и обратного поля (б).
в каждой точке воздушного зазора, расположенной на расстоянии


где

Это выражение можно преобразовать к виду:

Каждый из членов этой суммы представляет собой вращающуюся или бегущую волну НС. В данном случае образуются две вращающиеся в противоположные стороны волны НС: прямая волна





Расчет магнитной цепи постоянного магнита
Постоянные магниты широко применяются в измерительных приборах, реле, генераторах и т. д.

а) б)
Рис.1.4. Тороидальный магнитопровод с воздушным зазором (а) и его кривая размагничивания (б).

Если бы не было воздушного зазора, то, как видно из кривой размагничивания (рис.1.4б), напряженность в сердечнике равнялась бы нулю Hc=0, а индукция Bc в сердечнике равнялась бы остаточной индукции B0.
Из закона полного тока имеем:

Здесь

lc – длина средней линии тороида.
Напряженность магнитного поля в воздушном зазоре:

Если зазор достаточно мал, то можно пренебречь потоком рассеяния и считать, что поток в магните равен потоку в зазоре:

отсюда


Воспользовавшись выражением




коэффициент

Проведем прямую Hc= -NBc из точки 0 до пересечения с кривой размагничивания (рис.1.4б). Координаты точки пересечения

Расчет магнитный цепей
1. Расчет магнитный цепей
(общие сведения)

1.1. Магнитные цепи c постоянной магнитодвижущей силой
Магнитное поле представляет собой состояние материальной среды, обусловленное действием тока. Основной характеристикой магнитного поля является вектор магнитной индукции





где




У ферромагнитных материалов величина


Между напряженностью H и током I существует взаимосвязь, носящая название закона полного тока (второй закон Кирхгофа для магнитной цепи):

где

Если


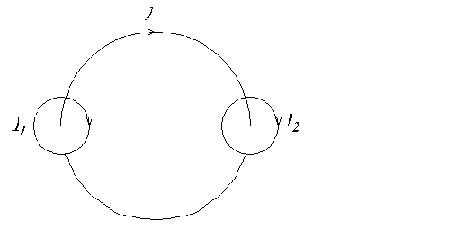


Рис.1.1. К закону полного тока (второй закон Кирхгофа для магнитной цепи).
Для катушек с числом витков wk имеем:

Единица измерения H [

Единица измерения B [Тл]; 1Тл=1

Магнитной цепью называют совокупность устройств, содержащих ферромагнитные тела, служащие для сосредоточения магнитного потока. Так как линии магнитной индукции замкнуты, то поток вектора магнитной индукции через замкнутую поверхность равен нулю:
Ф=

Из этого выражения следует:
в неразветвленной магнитной цепи поток Ф на всех участках одинаков, а в разветвленной цепи связь между потоками подчиняются первому закону Кирхгофа:
Ф1+Ф2+…


Если вектор магнитной индукции одинаков во всех точках сечения S неразветвленной цепи и направлен перпендикулярно этому сечению, то его поток Ф=

как

( индекс к указывает участок, где B и S неизменны). BК=

Подставив Bk в выражение полного тока, получим:


Отсюда получаем закон Ома для магнитной цепи:
Ф =

где
-


При неизменном S и


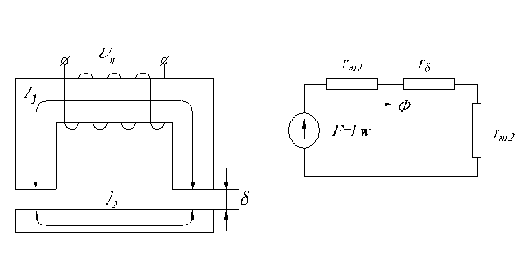

а) б)
Рис.1.2.Схема электромагнитного реле (а) и схема замещения его магнитной цепи (б).



При расчете этой цепи закон Ома может быть применен в случае, если ее можно свести к линейной, то есть при выполнении неравенства



Рис.1.3. Симметричная петля гистерезиса.
Ферромагнитные материалы с широкой петлей гистерезиса (Hc>4000


Основная кривая намагничивания ферромагнитного материала, которая приводится в справочниках – это кривая, проходящая через вершины семейства его петель гистерезиса.
При расчетах магнитной цепи решаются две задачи: а) прямая задача расчета, которая заключается в определении МДС Iw по заданному потоку и б) обратная задача, когда по заданному значению МДС требуется определить поток Ф.
При решении прямой задачи по заданному потоку определяют индукцию на каждом участке магнитной цепи. Затем, пользуясь основными кривыми намагничивания, находят напряженность Hk. Зная Hklk ,определяют МДС F=

Обратную задачу решают методом последовательного приближения. Задаваясь различными значениями потока Ф и рассчитав соответствующие значения МДС F, строят кривую Ф=f(F). По этой кривой для заданного значения F определяют искомое значение Ф.
Регулирование скорости вращения асинхронных двигателей
Скорость вращения асинхронного двигателя определяется зависимостью

Следовательно, ее можно регулировать, изменяя





Регулирование путем изменения частоты питающего напряжения. Применяемые ранее электромашинные преобразователи частоты очень громоздки, сложны в эксплуатации и дороги. Поэтому они практически полностью вытеснены полупроводниковыми преобразователями частоты, которые в настоящее время обеспечивают достаточную надежность в работе. При применении этого способа регулирования необходимо обеспечить (при изменении частоты питающей сети и питающего напряжения) постоянство потока намагничивания асинхронной машины.
Регулирование путем изменения числа пар полюсов позволяет получить ступенчатое изменение скорости вращения. Для двукратного изменения скорости отдельные катушки, составляющие данную фазу, переключаются с последовательного согласного соединения на встречное или с последовательного на параллельное. Обмотку ротора в этом случае выполняют короткозамкнутой. Если нужно иметь три или четыре скорости, то на статоре располагают еще одну обмотку, при переключении которой можно получить еще две скорости. Асинхронные электродвигатели с переключением числа пар полюсов называются многоскоростными. Недостатки этого способа регулирования скорости вращения: большие габариты и вес по сравнению с двигателями нормального исполнения, а, следовательно, и большая стоимость; большая величина ступеней регулирования (при частоте 50 Гц скорость вращения поля n, при переключениях изменяется в отношении 3000:1500:1000:750).
Регулирование путем включения в цепь ротора добавочных сопротивлений. Этот способ применяется для двигателей с фазовым ротором, он позволяет плавно изменять скорость вращения двигателя.
Недостатки: плохие энергетические характеристики асинхронной машины и чрезмерно “мягкая” механическая характеристика машины, что в некоторых случаях (при пульсациях нагрузочного момента) недопустимо.
Регулирование путем изменения питающего напряжения. Для двигателей нормального исполнения этот метод неприменим, т.к. пропорционально квадрату уменьшения напряжения питающей сети уменьшается величина момента двигателя. Он применяется для двигателей малой мощности, которые имеют значительные активные сопротивления роторной обмотки, т.к. в этом случае скольжение




2.4. Асинхронные исполнительные двигатели
Эти двигатели используются в устройствах автоматики, служат для преобразования подводимого к ним электрического сигнала в механическое перемещение вала. Исполнительные двигатели являются управляемыми двигателями. При заданном моменте нагрузки скорость двигателя должна строго соответствовать подводимому напряжению и меняться при изменении его величины и фазы. В качестве исполнительных двигателей применяются, главным образом, двухфазные асинхронные двигатели с короткозамкнутым ротором (рис. 2.19а).
|
|
|

Рис. 2.19. Принципиальная схема асинхронного исполнительного двигателя (а)
и векторные диаграммы его напряжений при амплитудном (б) и фазовом (в)
методах управления.
Одна из обмоток статора B, называемая обмоткой возбуждения, подключается к сети переменного тока с постоянным действующим значением напряжения


Различают три основных способа изменения напряжения на обмотке управления: амплитудное, фазовое и амплитудно-фазовое.
При амплитудном управлении изменяется лишь величина амплитуды напряжения управления или пропорциональное ей действующее значение



Векторы напряжений управления и возбуждения при всех значениях коэффициента







При амплитудно-фазовом управлении изменяется как амплитуда напряжения управления, так и угол сдвига фаз между напряжениями


При всех методах управления скорость асинхронного двигателя изменяется за счет создания несимметричного эллиптического магнитного поля.
Регулировочные характеристики
Эти характеристики показывают, как изменяется скорость исполнительного двигателя при изменении коэффициента сигнала, если момент (нагрузка) на валу двигателя остается неизменным. Уравнение регулировочной характеристики (2.74):

На рис.2.27 б показаны зависимости


Режим короткого замыкания трансформатора
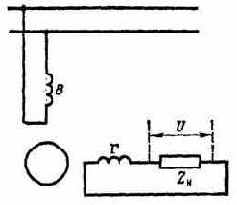
Режимом короткого замыкания называется режим, при котором вторичная обмотка замкнута накоротко. Если при опыте холостого хода определяются потери в сердечнике трансформатора, то при опыте короткого замыкания определяются потери в обмотках трансформатора. На первичную обмотку трансформатора подается напряжение такой величины, при которой ток в первичной цепи равен номинальному. При этом измеряется мощность, потребляемая трансформатором из сети, напряжение, ток (рис.1.22):

а)
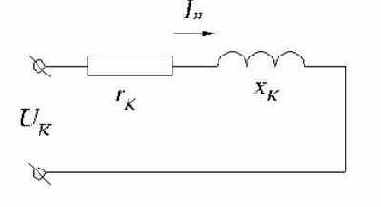
б)
Рис.1.22. Схемы измерения тока, напряжения и мощности в режиме к. з. трансформатора (а), схема замещения приведенного трансформатора в режиме к.з. (б).
Величина Uк составляет 5-10% номинального напряжения. Так как поток прямо пропорционален напряжению питания трансформатора, а потери в сердечнике пропорциональны квадрату потока, то в режиме короткого замыкания потерями в сердечнике можно пренебречь. Током холостого хода также пренебрегают, так как его величина незначительна по сравнению с Iном. Поэтому gn и bф в схеме замещения трансформатора в режиме короткого замыкания отсутствуют.
Параметры трансформатора определяются выражениями:

1.5.6. Падение напряжения в трансформаторе и его КПД
Для определения напряжения на нагрузке трансформатора воспользуемся его упрощенной схемой замещения без намагничивающего контура (рис.1.23а):


a) б)
Рис.1.23. Схема замещения приведенного трансформатора без учета контура намагничивания (а) и его векторная диаграмма в режиме нагрузки (б).
Погрешность определения тока I1, вызванная таким упрощением, при нагрузках, близких к номинальной, составляет величину порядка 0,1%, что вполне допустимо.
Обычно падение напряжения в трансформаторе определяется разностью вторичного напряжения трансформатора при холостом ходе U20 и





При холостом ходе отсутствуют падения напряжения в обмотках трансформатора. Поэтому, приняв



Эта величина называется относительной потерей напряжения. Ввиду того, что




Тогда

Из рис.1.23б получаем:



При номинальной нагрузке


или



где
Uka=


Для относительного падения напряжения, соответствующего току I1 получаем

где:

Так как

а


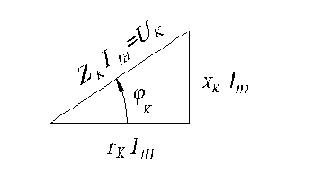
Рис.1.24. К расчету формулы 1.38.
то

Окончательно имеем

где


Рис.1.25 Внешняя характеристика трансформатора.
Высокие значения КПД трансформатора не позволяют определить его с достаточной точностью путем непосредственного измерения мощности, потребляемой от сети


Поэтому, согласно требованиям ГОСТа, его вычисляют косвенным методом по данным опытов холостого хода и короткого замыкания. Точность этого метода приемлема для практики.
Зависимость активной мощности трансформатора


При опыте холостого хода ток I10 невелик, и потерями мощности в первичной обмотке можно пренебречь. Следовательно, с достаточной степенью точности можно считать, что потери в сердечнике трансформатора определяются мощностью, потребляемой из сети при номинальном напряжении сети:

Из схемы замещения (без учета тока намагничивания) трансформатора имеем для режима к. з.:

Коэффициентом полезного действия трансформатора называют отношение отдаваемой мощности к мощности, потребляемой из сети:



Режим нагрузки трансформатора
Поток в магнитопроводе в режиме холостого хода трансформатора





(

При E1= U1 компенсация уменьшения потока производится за счет увеличения тока


Из уравнения видно, что увеличение





где

- составляющая первичного тока, уравновешивающая размагничивающее действие вторичного тока.
Таким образом, первичный ток равен векторной сумме тока холостого хода и приведенного вторичного тока. Ток холостого хода I10 составляет лишь несколько процентов от тока I1 в режиме номинальной нагрузки. Поэтому



Уравнения для первичной и вторичной цепей трансформатора:

Построение векторной диаграммы начинают с вектора магнитного потока













Чтобы построить вектор









-


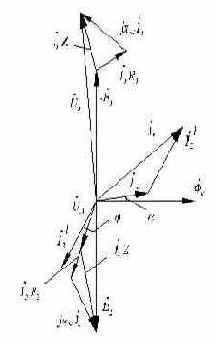
Рис.1.19. Векторная диаграмма трансформатора в режиме нагрузки.
Схема асинхронного тахогенератора.
На статоре в пазах уложены две обмотки, сдвинутые в пространстве на 90°.
По обмотке возбуждения проходит переменный ток, создавая магнитный поток Фd, пульсирующий с частотой сети f. Этот поток распределен в пространстве практически синусоидально, и ось его совпадает с осью обмотки возбуждения (рис. 5.28a), называемой продольной осью. Поэтому поток, создаваемый обмоткой возбуждения, называется продольным.
При неподвижном роторе магнитный поток Фd индуктирует в обмотке возбуждения ЭДС.

Пренебрегая активным сопротивлением обмотки возбуждения и индуктивным сопротивлением рассеяния можно записать:

Выходная обмотка расположена под углом 90° по отношению к обмотке возбуждения ЭДС в выходной обмотке, а значит и напряжение на нагрузке равно нулю. Часть потока в виду неидеальности симметрии наводит в выходной обмотке Г ЭДС называемую остаточной.
В каждом элементарном проводнике полого ротора пульсирующий поток индуктирует ЭДС











Рис. 5.28. Распределение ЭДС и токов в роторе при неподвижном (а) и вращающемся (б) роторе.
Как и в трансформаторе, появление МДС ротора приводит к появлению компенсирующего тока в обмотке возбуждения. При вращении ротора в элементарных проводниках помимо трансформаторной ЭДС



где
Вх – индукция в воздушном зазоре в рассматриваемой точке в данное мгновение;
Lv – длина ротора в магнитном поле;
V2 – окружная скорость ротора.
Поскольку поток Фd пульсирует с частотой f сети, то и индуктируемые им ЭДС

При синусоидальном законе распределения индукции Вх вдоль окружности ротора максимальное значение ЭДС












где

Очевидно, что частота ЭДС в выходной обмотке не зависит от скорости вращения ротора и при любых условиях равна частоте сети f.
Согласно закону Ома:

В асинхронной машине с полным немагнитным ротором воздушный зазор очень велик, магнитное сопротивление






Выходная характеристика асинхронного тахогенератора имеет вид (рис. 5.29):

Рис. 5.29. Выходные характеристики асинхронного тахогенератора при различных величинах нагрузки.
Причинами, вызывающими отклонение выходной характеристики от линейной зависимости являются:
а) технологические неточности при изготовлении;
б) электромагнитная реакция ротора, изменяющая величины потоков


в) изменение некоторых параметров тахогенератора при изменении скорости вращения (например, например сопротивление полого ротора);
г) изменение сопротивления обмоток и магнитного сопротивления машины по различным осям под влиянием температуры, насыщения и др.
Из-за технологических неточностей при изготовлении тахогенератора (отклонение обмоток В и Г от взаимного перпендикулярного положения, технологические неточности в величине воздушного зазора и толщине полого ротора) в выходной обмотке при скорости ротора, равной нулю, индуктируется некоторая остаточная ЭДС, называемая нулевым сигналом. Нулевой сигнал, обусловленный неточностью взаимного расположения обмоток В и Г, может быть уменьшен, если расположить обмотку возбуждения на внешнем статоре, а выходную обмотку – на внутреннем. Это дает возможность настроить тахогенератор на минимальный нулевой сигнал путем поворота внутреннего статора и установки его в такое положение, при котором остаточная ЭДС выходной обмотки будет минимальной. Другим способом уменьшения нулевого сигнала является включение обмоток статора по мостовой схеме (рис. 5.30).

Рис. 5.30. Мостовая схема включения обмоток асинхронного тахогенератора с компенсирующими элементами.
В этом случае между зажимами В и Г включают компенсирующее устройство, состоящее из емкости C и активного сопротивления R, величины которых подбирают так, чтобы в выходной обмотке индуктировалась минимальная остаточная ЭДС. При настройке тахогенератора стремятся получить минимальный нулевой сигнал при различных положениях ротора.
В идеальном тахогенераторе величина продольного магнитного потока Фd остается неизменной во всех режимах работы машины. В действительности этот поток изменяется при изменении, как скорости вращения, так и тока нагрузки в выходной обмотке. Это происходит по следующим причинам. Под действием потока Фq в элементах полого ротора индуктируется ЭДС вращения


При этом в машине появляется добавочная продольная составляющая намагничивающей силы ротора Fd2 , изменяющая ток в обмотке возбуждения


продольный поток

и ЭДС Е2 в выходной обмотке. Так как Фq пропорционален скорости вращения ротора, то ЭДС


При протекании тока нагрузки создается НС Fгq (рис. 5.31а).
В этом случае результирующая НС по поперечной оси





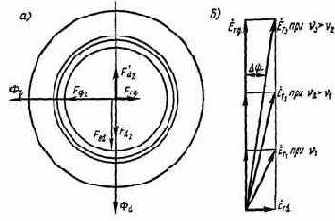
Рис. 5.31. Диаграмма пространственных векторов НС и потоков в асинхронном
тахогенераторе (а) и векторная диаграмма ЭДС, индуктированных в выходной
обмотке (б).
Из выражения для




Уравнение выходной характеристики тахогенератора Uвых = f (n) может быть получено путем разложения пульсирующего поля обмотки возбуждения на вращающиеся поля обратной и прямой последовательности:

где
n - относительная скорость вращения ротора;


Из этого выражения следует, что для уменьшения погрешности тахогенератора нужно уменьшать Вn2. С этой же целью тахогенераторы выбирают с большой синхронной скоростью, чтобы значение измеряемой скорости не превышало n=0,2….0,3; в связи, с чем они обычно выполняются на повышенную частоту питающей сети (400…500) Гц и с малым числом пар полюсов р.
Величина комплекса

где
r2 – активное сопротивление ротора;

Следовательно, при заданной нагрузке

Тахогенераторы большой точности работают при




Следовательно, амплитудная погрешность

а ее относительное значение

Фазовая погрешность:

где
Yвых.U и Yвых – фазы выходного напряжения, имеющие место при отсутствии и наличии комплекса В.
Обычно ЭДС EГq , индуктируемая в выходной обмотке поперечным потоком Фq , изменяется приблизительно пропорционально скорости вращения n; ЭДС ЕГd , индуктируемая продольным потоком

Наименьшая амплитудная погрешность имеет место при емкостной нагрузке, наименьшая фазовая – при индуктивной нагрузке.
Для устранения температурной погрешности в тахогенераторах большой точности ротор выполняют из материалов с весьма низким температурным коэффициентом сопротивления или применяют специальную температурную компенсацию.
Создание вращающегося магнитного поля
Индукция в воздушном зазоре электрической машины переменного тока определяется распределением НС вдоль окружности статора. Если пренебречь магнитным сопротивлением ферромагнитных участков магнитной цепи машины, то под кривой распределения НС




Сравнение исполнительных двигателей при различных методах управления
Проведенный анализ позволяет сделать следующие выводы:
а) линейность механических и регулировочных характеристик выше всего при фазовом управлении. Амплитудно-фазовое управление дает наибольшее отклонение от прямой линии.
б) Мощность управления при амплитудном и амплитудно-фазовом управлении практически одинакова и пропорциональна квадрату коэффициента сигнала.
в) степень использования (электромагнитная мощность при круговом поле и неподвижном роторе) для всех трех способов управления одинакова, если одинаково напряжение возбуждения.
г) наиболее простым является амплитудно-фазовое управление (конденсаторная схема), при котором не требуется никаких дополнительных устройств для сдвига фаз между напряжениями управления и возбуждения. Это обстоятельство и объясняет широкое применение его в автоматике.
3. Синхронные электрические машины.
3.1. Общие сведения
Электромагнитная схема синхронной машины имеет вид (рис3.1):
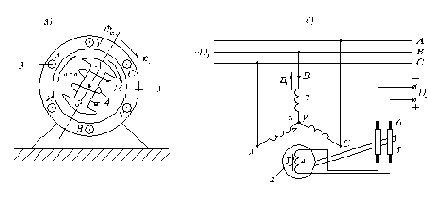
Рис. 3.1. Электромагнитная схема синхронной машины (а) и схема ее включения (б).
Важным отличием синхронной машины от асинхронной является то, что главный магнитный поток в ней создается НС постоянного тока возбуждения Iв , который машина получает от источника Uв, т. е. в машине имеет место раздельное питание обмоток статора и ротора.
Статор машины выполнен аналогично статору асинхронной машины. На нем расположена

При вращении ротора со скоростью n2 в обмотке статора индуктируется ЭДС

f1=(pn2)/60, (3.1.1)
где
p – число пар полюсов машины.
При подключении обмотки статора к какой-либо нагрузке в ней протекает многофазный ток, который создает вращающееся магнитное поле. Скорость вращения этого поля:
n1=(60f1)/p. (3.1.2)
Из приведенных выше выражений следует n1=n2, т. е. магнитные поля ротора и статора вращаются с одинаковой скоростью. Поэтому рассматриваемая машина получила название синхронной. В синхронной машине результирующий магнитный поток Фрез создается совместным действием намагничивающих сил обмотки возбуждения и обмотки статора и вращается с той же скоростью, что и ротор.
Часть электрической машины, в которой индуктируется ЭДС, принято называть якорем, поэтому в синхронной машине статор является якорем, а ротор – индуктором. Синхронная машина может работать в качестве автономного генератора, питающего подключенную к ней нагрузку, а так же подключаться параллельно к сети, к которой присоединены другие генераторы. При работе параллельно с сетью она может отдавать или потреблять электрическую энергию, т.е. работать генератором или двигателем. В результате взаимодействия тока ротора Iв с вращающимся магнитным полем, создается электромагнитный момент, который при работе машины в двигательном режиме является вращающим, а в генераторном – тормозящим.
Таким образом, синхронная машина имеет следующие особенности:
- ротор машины, как в двигательном, так и в генераторном режимах, вращается с постоянной скоростью, равной скорости вращения магнитного поля;
- частота изменения ЭДС Е1, индуктируемой в обмотке статора, пропорциональна скорости вращения ротора;
- в обмотке ротора ЭДС не индуктируется, а магнитное поле создается постоянным током, подводимым от внешнего источника, или постоянными магнитами.
Постоянство скорости вращения ротора синхронной машины обусловливает область ее применения: в качестве генераторов промышленной частоты на подстанциях или в дизель – генераторах, а в качестве двигателей в тех случаях, когда необходимо постоянство скорости вращения выходного вала машины.
В случае параллельной работы с другими синхронными машинами для включения синхронной машины в общую сеть требуется предварительная синхронизация, т. е. частота выходного напряжения должна быть строго равна частоте сети, а ЭДС машины – равной по величине и противоположной по фазе напряжению сети. При идеальной синхронизации машины с сетью токи в обмотках статора после подключения машины к сети, будут равны нулю. В таких условиях синхронная машина не отдает энергию в сеть и не потребляет ее, т. е. по отношению к сети она не является ни генератором, ни двигателем. Собственные потери синхронной машины, механические и магнитные, при этом покрывает первичный двигатель.
Если увеличивать момент, приложенный первичным двигателем к валу машины, то под действием возросшего момента ротор машины сместится вперед, и если раньше середина полюса ротора находилась против проводников данной фазы статора как раз в тот момент, когда напряжение сети на этой фазе достигло своего максимума, то теперь это условие нарушается, и так как ЭДС ротора и напряжение сети уже взаимно не уравновешиваются, то в обмотках статора возникает ток, создаваемый результирующим напряжением. Взаимодействие этого тока с полем машины создает тормозящую силу, воздействующую на ротор. При посредстве этой силы механическая мощность первичного двигателя будет превращаться в электрическую мощность, отдаваемую генератором в сеть. Поле ротора будет как бы вести за собой поле статора.
Если затем уменьшать вращающий момент на валу синхронной машины, то под действием тормозящего момента электромагнитных сил поле ротора будет уменьшать свой угол опережения по отношению к полю статора, и вместе с уменьшением угла между осями полей будет уменьшаться и тормозящая сила взаимодействия токов статора и поля машины.
Наконец, когда напряжение сети будет уравновешиваться ЭДС статора, тогда машина перестанет отдавать энергию в сеть, ток в обмотке статора, а, следовательно, и тормозящая электромагнитная сила, становится равной нулю.
Если теперь приложить к валу машины вместо вращающего тормозящий момент механической нагрузки, то ротор сместится по отношению к вращающему полю в сторону отставания. Вновь возникнут токи в обмотках статора и создадут электромагнитные силы взаимодействия токов статора и поля ротора, но на этот раз силы будут стремиться сместить ротор вперед, т. е. создадут вращающий момент, при посредстве которого электрическая мощность сети превращается в механическую мощность на валу машины; таким путем синхронная машина переходит к работе двигателем. Режим машины меняется от генераторного к двигательному и обратно в зависимости от механического воздействия на вал машины, причем электромагнитные силы играют роль своеобразной упругой связи между полем ротора и полем статора. Можно сравнить их с пружинами, связывающими два шкива А и В – ведущий и ведомый (рис. 3.2).



а) б) в)
Рис. 3.2. Механическая модель образования синхронного момента в виде двух шкивов, соединенными пружинами ((а) – нет передачи энергии; (б) – передача энергии от шкива А к шкиву В; (в) – передача энергии от шкива В к шкиву А).
Шкив изображает в такой модели поле ротора, шкив В – поле статора. Всякое изменение механической силы на валу шкива А вызывает изменение относительного положения шкивов и изменение направления и степени натяжения пружин. При



Таким образом, при параллельной работе синхронной машины с сетью скорость вращения машины жестко определяется частотой сети; изменение момента на валу меняет лишь угол между осями полей ротора и статора, в то время как в асинхронной машине в таких условиях меняется скорость вращения ротора (скольжение).
Реакция якоря в синхронном генераторе. Магнитное поле нагруженной синхронной машины возбуждается не только НС ротора, на это поле действует НС обмотки якоря, обтекаемой нагрузочным током.
В асинхронной машине ток статора изменяется автоматически вслед за изменение тока ротора и, таким образом, сохраняется практически постоянным поток в воздушном зазоре. В синхронной машине изменение тока статора не вызывают автоматического изменения постоянного тока возбуждения. Поэтому результирующее магнитное поле синхронной машины изменяется с изменением нагрузки, меняется относительное положение вращающегося поля статора к вращающемуся полю ротора, а, следовательно, и характер реакции якоря. Если рассматривать синхронный генератор, то при активной нагрузке ток в фазе статора достигает максимума в тот момент, когда против этой фазы находится середина полюса (3.3а).

a) б) в)
Рис. 3.3. Реакция якоря и кривые распределения индукций в неявнополюсной машине при различных условиях нагрузки.
Поле статора будет в этом случае поперечным, ось потока полюсов ротора перпендикулярна оси поля статора – у набегающего конца полюса оно направлено против поля ротора и ослабляет это поле, а у сбегающего конца поля оно усиливает поле ротора. Реакция якоря в случае активной нагрузки генератора вызывает смещение оси результирующего поля в сторону вращения. Результирующий поток при этом несколько изменяется вследствие влияния насыщения, а именно, он ослабляется у набегающего конца полюса больше, чем усиливается у сбегающего.
В идеальном случае чисто индуктивной нагрузке генератора (3.3б) величина тока в фазе статора будет достигать своего максимального значения только тогда, когда соответствующий полюс ротора уйдет вперед на 90 градусов; при индуктивной нагрузке поток статора направлен вдоль полюса ротора против потока ротора.
Следовательно, при индуктивной нагрузке НС тока статора стремится возбудить размагничивающий продольный поток.
В идеальном случае чисто емкостной нагрузке генератора (3.3в) ток статора будет достигать максимума тогда, когда соответствующий полюс ротора будет находиться еще на расстоянии 90 градусов от середины фазы. В этом случае поток ротора будет намагничивающим продольным.
Условие синусоидальности распределения поля статора вдоль окружности статора существенно нарушается в случае явнополюсных роторов, у которых распределение поля статора вдоль окружности статора далеко не синусоидально.
Следовательно, в синхронной машине реакция якоря вызывает изменение магнитного поля машины и в результате – изменение ее ЭДС. В машинах с явными полюсами это явление еще осложняется искажением кривой ЭДС. Для синхронных генераторов подобное влияние величины тока и сдвига фаз нагрузки на напряжение машины весьма нежелательно. Чтобы свести влияние реакции якоря к минимуму, необходимо, чтобы НС якоря была мала по сравнению с НС ротора. Для осуществления этого условия необходимо увеличить магнитное сопротивление машины.
Лучше и проще всего повышение магнитного сопротивления осуществляется путем увеличения воздушного зазора машины. Однако при этом необходимо соответствующее увеличение НС ротора, но в синхронной машине это увеличение намагничивающего тока допустимо, т. к. энергия магнитного поля ротора остается неизменной, а возбудитель синхронной машины должен давать энергию только для покрытия тепловых потерь в цепи ротора. В асинхронной машине условия иные, там намагничивающий ток должен поддерживать колебания энергии магнитного поля машины – он является реактивным током, ухудшающим cos? установки, и желательно сделать его возможно меньшим.
Явление реакции якоря относится и к синхронным двигателям, но, т. к. в этих двигателях форма кривой ЭДС практически малосущественна, то реакция якоря в них имеет второстепенное значение.
3.1.1. Векторные диаграммы синхронного генератора
Результирующий магнитный поток в синхронном генераторе можно разложить на поток ротора, поток рассеяния статора и поток реакции якоря. Поток рассеяния статора является частью потока статора, замыкающегося помимо ротора поперек пазов статора. Этот поток проходит значительную часть своего пути в воздухе, поэтому его можно считать пропорциональным току статора и совпадающим с этим током по фазе.
Если не учитывать влияние насыщения стали, то поток реакции якоря, так же как и поток рассеяния пропорционален току якоря (статора)

При принятых допущениях ЭДС







Следовательно,


Рис. 3.4. Векторная диаграмма синхронной машины в режиме генератора.
Поток ротора








где
xH и RH – индуктивное и активное сопротивление цепи нагрузки генератора.
Чтобы определить положение вектора










3.1.2. Электромагнитный момент синхронной машины
Для получения выражения электромагнитного момента синхронной машины рассмотрим ее векторную диаграмму в несколько упрощенном виде (рис 3.5):

Рис. 3.5. К определению электромагнитного момента синхронной машины.
Построение упрощенной векторной диаграммы начнем с вектора напряжения сети










Положение вектора потока ротора




т. е. напряжение равно сумме ЭДС, индуктируемых в обмотке якоря тремя потоками машины. Но физически эти потоки образуют один результирующий магнитный поток




Угол между векторами




Мощность синхронной трехфазной машины:

Из прямоугольного треугольника, гипотенузой которого является вектор



На основании той же векторной диаграммы

Это дает возможность представить электрическую мощность синхронной машины в
виде:

Электромагнитный момент синхронной машины:

Эта зависимость носит название угловой характеристики синхронной машины (рис. 3.6).

Рис. 3.6. Угловая характеристика синхронной машины.
Если ?>0, то мощность и момент положительны, машина работает в режиме генератора и отдает электрическую мощность, а электромагнитный момент при этом является тормозящим моментом, который преодолевает первичный двигатель. Работа, совершаемая первичным двигателем, преобразуется в электрическую работу, отдаваемую генератором в сеть. При увеличении создаваемого первичным двигателем вращающего момента, ротор машины, вследствие сообщаемого ему ускорения, увеличивает угол ? и после нескольких колебаний около синхронной скорости восстанавливается равновесие вращающегося момента первичного двигателя и тормозящего электромагнитного момента генератора. Таким же образом восстанавливается это равновесие при уменьшении вращающего момента первичного двигателя посредством уменьшения угла ? и вызываемого этим снижения тормозящего электромагнитного момента.
Работа синхронного генератора устойчива при изменении угла ? в пределах от 0 до 90 градусов.
Кривая Мэ.м.=F(?) за точкой ?=90 соответствует области неустойчивой работы синхронного генератора. В этих условиях вращающий момент первичного двигателя превышает максимальный тормозящий момент генератора, т. к. увеличение ? свыше 90 приводит к уменьшению тормозящего электромагнитного момента Мэ.м. Избыток вращающего момента создает дальнейшее ускорение ротора, что обуславливает дальнейшее возрастание ? и новое уменьшение тормозящего момента и т.
д. пока генератор не выпадет из синхронизма. В таком случае нарушается автоматическая связь между частотой сети и скоростью вращения ротора; ЭДС машины и напряжение сети перестают уравновешивать друг друга, и токи в обмотках статора могут достигнуть весьма больших значений токов короткого замыкания, т. к. мгновенные значения ЭДС статора и напряжение сети могут теперь складываться, а не вычитаться, как при нормальной работе. При выпадении генератора из синхронизма его отключают от сети приборы автоматической защиты.
Уменьшение вращающего момента первичного двигателя вызывает соответствующее уменьшение угла ?, и когда ? станет равным нулю, тогда первичный двигатель будет лишь покрывать потери синхронной машины; в этих условиях при ?=0 машина не будет отдавать энергию в сеть как генератор и потреблять ее из сети как двигатель. Этот режим является промежуточным между режимами генератора и двигателя.
Если приложить к валу синхронной машины тормозящий момент, то он вызовет некоторое замедление вращения ротора, вследствие чего угол ? станет отрицательным. Это значит, что ротор отстанет на угол ?/р от результирующего поля машины, и последнее станет ведущим, а ротор – ведомым. Перемена знака ? вызовет изменение знака электрической мощности Р и электромагнитного момента Мэ.м.; машина переходит в режим двигателя; она потребляет энергию из сети, ее электромагнитный момент стал вращающим моментом, уравновешивающим механический тормозящий момент, приложенный к валу машины.
В этом случае для построения упрощенной векторной диаграммы синхронного двигателя удобно использовать векторы



Рис. 3.7. Упрощенная векторная диаграмма синхронного двигателя.
Будем считать, что возбуждение машины при переходе от генераторного режима к двигательному осталось неизменным, и поэтому сохраним в диаграмме двигателя, как и в диаграмме генератора, ту же длину вектора










Теперь









Режим двигателя устойчив при изменении ? в пределах от 0 до -90 и неустойчив при ?<-90 градусов, когда возрастание ? не увеличивает, а уменьшает вращающий момент. Если механический тормозящий момент, приложенный к валу двигателя, превзойдет максимальное значение вращающего электромагнитного момента Мэ.м.max, то произойдет выпадение двигателя из синхронизма – ротор постепенно уменьшит скорость и, наконец, остановится, ЭДС в обмотке уменьшится до 0, а токи достигнут весьма больших значений, во много раз превышающих номинальные. Автоматическая защита отключит двигатель от питания сети.
Работающая параллельно с сетью синхронная машина нагружается как в режиме двигателя, так и в режиме генератора, путем изменения момента, приложенного к валу. Практически используется только кратковременный переход двигателя в режим генератора для быстрого торможения двигателя.
Величина

называется синхронизирующей мощностью, а величина

- синхронизирующим моментом.
Практически синхронная машина работает сравнительно далеко от предела статической устойчивости, соответствующего ?=90 градусов. У синхронных генераторов угол ? при номинальной нагрузке не превышает 20 градусов, а у двигателей, как менее ответственной машины, этот угол достигает 30 градусов.
Форма угловой характеристики синхронной машины объясняется картиной взаимодействия потоков Фв и Ф в синхронной машине (рис. 3.8).

Рис. 3.8. Картина взаимодействия потоков





При ?=0 (рис.3.8а) между ротором и статором существует только сила притяжения (между двумя магнитами). Тангенциальная составляющая силы равна 0, Поэтому электромагнитный момент равен 0 .
При ?>0 (рис.3.8б) ось потока возбуждения опережает ось результирующего потока на угол ?, вследствие чего тангенциальная составляющая силы создает тормозной момент для внешнего двигателя, приводящего во вращение ротор синхронного генератора. Максимум тормозного момента соответствует ?=90 градусов, когда ось полюсов ротора расположена между осями полюсов статора. При ?<0 (рис.3.8в) (режим двигателя) ось потока возбуждения отстает от оси результирующего потока. Поэтому, возникающие при этом тангенциальные силы создают вращающий момент, который приводит во вращение ротор синхронной машины.
Подключение синхронной машины к сети. При подключении синхронного генератора применяют два способа: точная синхронизация и самосинхронизация.
Первый способ требует предварительную синхронизацию включаемого генератора, которая осуществляется следующим образом (рис. 3.9).

Рис. 3.9. Схема подключения синхронного генератора к сети с помощью лампового синхроноскопа.
Скорость машины Г доводится примерно до синхронного числа оборотов и ее возбуждение регулируется так, чтобы вольтметр на ее зажимах показал значение, равное напряжению сети. При этом последовательность фаз машины должна соответствовать последовательности фаз сети. Перед подключением машины к сети необходимо более точное регулирование частоты вращения машины и фазы ее ЭДС. Для этой цели используют синхроскопы. В простейшем случае синхроскоп составляется из ламп накаливания. Чем меньше частота генератора отличается от частоты сети, тем медленнее будут происходить колебания света фазных ламп. Достигают совпадения частот, при котором промежутки времени между следующими друг за другом вспышками ламп будут не менее 3…5 сек. Затем в момент полного затухания ламп замыкается рубильник.
Сущность метода самосинхронизации состоит в том, что генератор включается на сеть без возбуждения, когда его скорость отличается от синхронной на 2…3%. Обмотка ротора во время такого включения должна быть замкнута накоротко или на некоторое сопротивление.
Сейчас же после включения генератора на сеть в ротор подается постоянный ток возбуждения, и генератор сам доходит до синхронной скорости под действием электромагнитных сил.
Вращающий момент синхронного двигателя при пуске равен 0, поэтому пуск двигателя состоит из двух этапов: первый этап – синхронный пуск с помощью короткозамкнутой обмотки, расположенной на роторе, и второй этап – втягивание в синхронизм после включения постоянного тока возбуждения. Во время первого этапа асинхронного пуска обмотка возбуждения отключается от источника постоянного тока и замыкается на активное сопротивление, превышающее активное сопротивление обмотки возбуждения в 10…15 раз. Не следует оставлять обмотку возбуждения разомкнутой, т. к. вращающееся поле может индуктировать в ней весьма значительную ЭДС, опасную для изоляции. Но с другой стороны, нецелесообразно было бы замыкать эту обмотку накоротко, т. к. в ней возникает значительный однофазный ток, который будет тормозить ротор по достижении им половины синхронной скорости.
3.2. Реактивный двигатель
Реактивным двигателем называется синхронный двигатель без обмотки возбуждения и без постоянных магнитов. Вращающий момент в таких двигателях возникает вследствие различия магнитных проводимостей по продольной и поперечной осям машины (рис. 3.10).

Рис. 3.10. Схема, иллюстрирующая возникновение реактивного момента.

Статор синхронной реактивной машины выполняется, так же как и статор обычной машины переменного тока.
Рис.3.11. Конструкции ротора
Ротор собирается из стальных листов специального профиля (рис.3.11).
На его валу расположена короткозамкнутая обмотка для асинхронного пуска синхронного реактивного двигателя.
Электромагнитный момент синхронного реактивного двигателя выражается следующей зависимостью:

где
xd и xq – синхронные индуктивные сопротивления по продольной и поперечной осям машины.
Начальный пусковой момент у этих двигателей равен 0. Поэтому в них применяется асинхронный способ пуска, для чего используется короткозамкнутая обмотка на роторе.
Реактивные двигатели проще по конструкции, дешевле и надежнее в эксплуатации, чем обычные синхронные машины с обмоткой возбуждения на роторе.
Основные недостатки двигателей: низкий cos? и КПД, большие размеры, малая величина максимального момента. В двигателе мощностью несколько десятков ватт КПД составляет 0,3…0,4, а мощностью до 10 ватт – менее 0,2.
Так как момент двигателя пропорционален U2, то двигатель чувствителен к колебаниям питающего напряжения.
Угловая характеристика реактивного двигателя изображена на рис. 3.12.

Рис. 3.12. Угловая характеристика реактивного двигателя.
3.3. Гистерезисный двигатель
Гистерезисным двигателем называется синхронный двигатель, в котором вращающий момент создается за счет явления гистерезиса при перемагничивания ферромагнитного материала ротора. Статор гистерезисного двигателя подобен статору обычной машины переменного тока. Ротор представляет собой стальной цилиндр из ферромагнитного магнитотвердого материала (имеющего широкую петлю гистерезиса) без обмотки. С целью удешевления ротор делают сборным: кольцо из ферромагнитного материала и немагнитная или магнитомягкая втулка (рис.3.13.а).
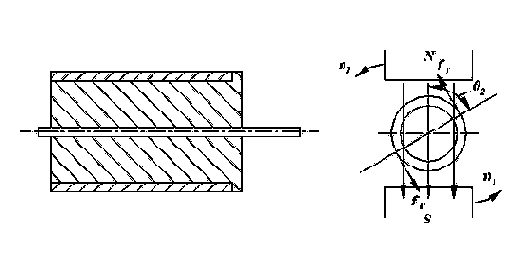
а) б)
Рис. 3.13. Устройство гистерезисного двигателя (а) и схема, иллюстрирующая возникновение гистерезисного момента (б).
В гистерезисном двигателе ротор, вращающийся с синхронной скоростью, представляет собой постоянный магнит. Ось магнита из-за явления гистерезиса отстает от оси вращающегося магнитного поля на угол ?г гистерезисного сдвига, вследствие чего возникает тангенциальная составляющая fг сил взаимодействия между полюсами ротора и потоком статора (рис. 3.13б). Величина силы fг и создаваемый ею момент не зависят от скорости вращения, а определяются шириной петли гистерезиса ферромагнитного материала.

|
Рис.3.14. Зависимость моментов гистерезисного двигателя от скольжения.
Если нагрузочный момент больше Мг (рис.3.14), то двигатель перейдет в асинхронный режим работы, т.е. появится дополнительный асинхронный момент Ма. Асинхронный момент Ма есть результат взаимодействия вращающегося магнитного поля с вихревыми токами, которые индуктируются этим полем в сердечнике ротора. Т к. ротор имеет большое активное сопротивление, то характеристика Ма=f(s) практически линейна и асинхронный гистерезисный момент максимален при s=1.



где
П2Н – потери на перемагничивание ротора при неподвижном роторе;
Пвихр.Н – потери на вихревые токи при неподвижном роторе;
Гистерезисные двигатели могут работать как в асинхронном, так и в синхронном режиме. Однако, в асинхронном режиме КПД двигателя резко уменьшается:
П=Пг+Пвихр=sП2Н+s2Пвихр.Н .

Достоинства гистерезисного двигателя: простота, надежность, плавность входа в синхронизм, бесшумность, малый пусковой ток, сравнительно высокий КПД (до 60%).
Недостатки: дороговизна, склонность к качаниям при резких изменениях нагрузки.
Мощность до 2000 Вт, частота f=50, 400 и 500 Гц.
3.4. Синхронные шаговые двигатели
В системах управления электроприводами с применением уже рассмотренных нами типов двигателей для отработки заданного угла или перемещения используют датчики обратной связи по углу или положению выходного вала исполнительного двигателя (рис. 3.15).
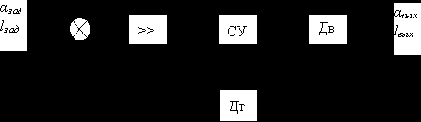
Рис.3.15. Система отработки угла (положения) выходного вала двигателя с использованием датчика обратной связи.
Если в качестве исполнительного двигателя использовать синхронный шаговый двигатель, то можно обойтись без датчика обратной связи (Дт) и упростить систему управления двигателем (СУ), так как отпадает необходимость использования в ней цифро-аналоговых (ЦАП) и аналого-цифровых (АЦП) преобразователей.
Шаговыми двигателями называются синхронные двигатели, преобразующие команду, заданную в виде импульсов, в фиксированный угол поворота двигателя или в фиксированное положение подвижной части двигателя без датчиков обратной связи.
Мощность шаговых двигателей лежит в диапазоне от единиц ватт до одного киловатта.
Шаговый двигатель имеет не менее двух положений устойчивого равновесия ротора в пределах одного оборота.
Напряжение питания обмоток управления шагового двигателя представляет собой последовательность однополярных или двуполярных прямоугольных импульсов, поступающих от электронного коммутатора (К). Результирующий угол соответствует числу переключений коммутатора, а частота вращения двигателя соответствует частоте переключений электронного коммутатора.
Шаговые двигатели различаются по конструктивным группам: активного типа (с постоянными магнитами), реактивного типа и индукторные.
Шаговые синхронные двигатели активного типа. В отличие от синхронных машин
непрерывного вращения шаговые двигатели имеют на статоре явно выраженные
полюса, на которых расположены катушки обмоток управления.

Рис. 3.16. Принципиальная схема управления шаговым двигателем.
Различают два вида коммутации обмотки шагового двигателя: симметричная и несимметричная.
При симметричной системе коммутации на всех четырех тактах возбуждается одинаковое число обмоток управления (рис. 3.17).
 |
Рис.3.17. Симметричная система коммутации.
 |
|||
 |




Рис.3.18. Несимметричная система коммутации.
Ротор у шагового двигателя активного типа представляет собой постоянный магнит (рис. 3.4.5), при числе пар полюсов больше 1, выполненный в виде «звездочки» (рис. 3.4.6).
Число тактов КТ системы управления называют количеством состояний коммутатора на периоде его работы T. Как видно из рисунков для симметричной системы управления КТ =4, а для несимметричной КТ =8.
В общем случае число тактов КТ зависит от числа обмоток управления (фаз статора) mу и может быть посчитано по формуле:

где
n1=1 при симметричной системе коммутации;
n1=2 при несимметричной системе коммутации;
n2=1 при однополярной коммутации;
n2=2 при двуполярной коммутации.

Рис. 3.19. Схемы, иллюстрирующие положения ротора шагового двигателя с постоянными магнитами при подключении к источнику питания одной (а) и двух обмоток (б).
При однополярной коммутации ток в обмотках управления протекает в одном направлении (рис. 3.19а); при двуполярной – в обеих (рис. 3.19б).
Синхронизирующий (электромагнитный) момент машины является результатом взаимодействия потока ротора с дискретно вращающимся магнитным полем статора. Под действием этого момента ротор стремится занять такое положение в пространстве машины, при котором оси потоков ротора и статора совпадают.
Мы рассмотрели шаговые синхронные машины с одной парой полюсов (р=1).
Реальные шаговые микродвигатели являются многополюсными (р>1).
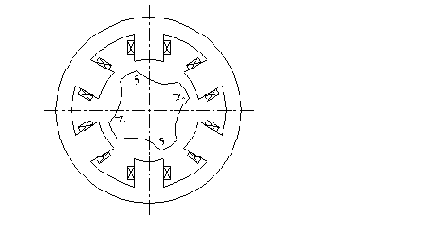
Рис. 3.20. Двуполюсный трехфазный шаговый двигатель.
Двигатель с р парами полюсов имеет зубчатый ротор в виде звездочки с равномерно расположенными вдоль окружности 2р постоянными магнитами. Для многополюсной машины величина углового шага ротора равна:

Чем меньше шаг машины, тем точнее (по абсолютной величине) будет отрабатываться угол. Увеличение числа пар полюсов связано с технологическими возможностями и увеличением потока рассеяния. Поэтому р= 4…6.
Величина

Реактивные шаговые двигатели. У активных шаговых двигателей есть один существенный недостаток: у них крупный шаг, который может достигать десятков градусов.
Реактивные шаговые двигатели позволяют редуцировать частоту вращения ротора. В результате можно получить шаговые двигатели с угловым шагом, составляющим доли градуса.
Отличительной особенностью реактивного редукторного двигателя является расположение зубцов на полюсах статора (рис.3.21).
а) б)

Рис. 3.21. Принцип действия реактивного редукторного шагового двигателя: (а) – исходное положение устойчивого равновесия; (б) – положение устойчивого равновесия. cдвинутое на один шаг (

Если зубцы ротора соосны с одной диаметрально расположенной парой полюсов статора, то они сдвинуты относительно каждой из оставшихся трех пар полюсов статора соответственно на ¼, ½ и ¾ зубцового деления.
При большом числе зубцов ротора Zр его угол поворота значительно меньше угла поворота поля статора.
Величина углового шага редукторного реактивного шагового двигателя определится выражением:

В выражении для КТ величину n2 следует брать равной 1, т. к. изменение направления поля не влияет на положение ротора.
Электромагнитный синхронизирующий момент реактивного двигателя обусловлен, как и в случае обычного синхронного двигателя, разной величиной магнитных сопротивлений по продольной и поперечной осям двигателя.
Основным недостатком шагового реактивного двигателя является отсутствие синхронизирующего момента при обесточенных обмотках статора.
Повышение степени редукции шаговых двигателей, как активного типа, так и реактивного, можно достичь применением двух, трех и многопакетных конструкций. Зубцы статора каждого пакета сдвинуты относительно друг друга на часть зубцового деления. Если число пакетов два, то этот сдвиг равен 1/2 зубцового деления, если три, то - 1/3, и т.д. В то же время роторы-звездочки каждого из пакетов не имеют пространственного сдвига, т.е. оси их полюсов полностью совпадают.
Такая конструкция сложнее в изготовлении и дороже однопакетной, и, кроме того, требует сложного коммутатора.
Индукторные (гибридные) шаговые двигатели. Стремление совместить преимущества активного шагового двигателя (большой удельный синхронизирующий момент на единицу объема, наличие фиксирующего момента) и реактивного шагового двигателя (малая величина шага) привело к созданию гибридных индукторных шаговых двигателей.
В настоящее время имеется большое число различных конструкций индукторных двигателей, различающихся числом фаз, размещением обмоток, способом фиксации ротора при обесточенном статоре и т.д. Во всех конструкциях индукторных шаговых двигателей вращающий момент создается за счет взаимодействия магнитного поля, создаваемого обмотками статора и постоянного магнита в зубчатой структуре воздушного зазора. При этом синхронизирующий момент шагового индукторного двигателя по природе является реактивным и создается намагничивающей силой обмоток статора, а постоянный магнит, расположенный либо на статоре, либо на роторе, создает фиксирующий момент, удерживающий ротор двигателя в заданном положении при отсутствии тока в обмотках статора.
По сравнению с шаговым двигателем реактивного типа у индукторного шагового двигателя при одинаковой величине шага больше синхронизирующий момент, лучшие энергетические и динамические характеристики.
Линейные шаговые синхронные двигатели. При автоматизации производственных процессов весьма часто необходимо перемещать объекты в плоскости (например, в графопостроителях современных ЭВМ и т.д.). В этом случае приходится применять преобразователь вращательного движения в поступательное с помощью кинематического механизма.
Линейные шаговые двигатели преобразуют импульсную команду непосредственно в линейное перемещение. Это позволяет упростить кинематическую схему различных электроприводов (рис. 3.22).

Рис. 3.22. Схема, иллюстрирующая работу линейного шагового двигателя.
Статор линейного шагового двигателя представляет собой плиту из магнитомягкого материала. Подмагничивание магнитопроводов производится постоянным магнитом.
Зубцовые деления статора и подвижной части двигателя равны. Зубцовые деления в пределах одного магнитопровода ротора сдвинуты на половину зубцового деления ?/2. Зубцовые деления второго магнитопровода сдвинуты относительно зубцовых делений первого магнитопровода на четверть зубцового деления ?/4. Магнитное сопротивление потоку подмагничивания не зависит от положения подвижной части.
Принцип действия линейного шагового двигателя не отличается от принципа действия индукторного шагового двигателя. Разница лишь в том, что при взаимодействии потока обмоток управления с переменной составляющей потока подмагничивания создается не момент, а сила FС, которая перемещает подвижную часть таким образом, чтобы против зубцов данного магнитопровода находились зубцы статора, т.е. на четверть зубцового деления ?/4.

где
KТ – число тактов схемы управления.
Для перемещения объекта в плоскости по двум координатам применяются двухкоординатные линейные шаговые двигатели.
В линейных шаговых двигателях применяют магнито-воздушную подвеску. Ротор притягивается к статору силами магнитного притяжения полюсов ротора. Через специальные форсунки под ротор нагнетается сжатый воздух, что создает силу отталкивания ротора от статора. Таким образом, между статором и ротором создается воздушная подушка, и ротор подвешивается над статором с минимальным воздушным зазором. При этом обеспечивается минимальное сопротивление движению ротора и высокая точность позиционирования.
Режимы работы синхронного шагового двигателя. Шаговый двигатель работает устойчиво, если в процессе отработки угла при подаче на его обмотки управления
серии импульсов не происходит потери ни одного шага. Это значит, что в процессе отработки каждого из шагов ротор двигателя занимает устойчивое равновесие по отношению к вектору результирующей магнитной индукции дискретно вращающегося магнитного поля статора.
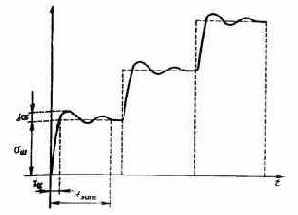

Рис.3.23. Процесс отработки шагов шаговым двигателем.
При этом возможны колебания углового вала двигателя относительно установившегося значения. Эти колебания обусловлены запасом кинетической энергии, которая была накоплена валом двигателя при отработке угла. Кинетическая энергия преобразуется в потери: механические, магнитные и электрические. Чем больше величина перечисленных потерь, тем быстрее заканчивается переходный процесс отработки единичного шага двигателем.
В процессе пуска ротор может отставать от потока статора на шаг и более; в результате может быть расхождение между числом шагов ротора и потока статора.
Основными характеристиками шагового двигателя являются: шаг, предельная механическая характеристика и приемистость.

Рис. 3.24. Предельная механическая характеристика шагового двигателя.
С увеличением частоты управляющих импульсов величина максимального момента падает, что объясняется действием демпфирующего момента (вызванного перечисленными выше потерями), и ЭДС самоиндукции становится соизмеримой с напряжением источника питания.

Рис.3.25. Предельная динамическая характеристика шагового двигателя.
Приемлемость падает с увеличением нагрузки.
.
4. Машины постоянного тока
4.1. Устройство, принцип действия и электромагнитный
момент машины постоянного тока
Устройство машины постоянного тока подобно обращенной синхронной машине, у которой обмотка якоря расположена на роторе, а обмотка возбуждения – на статоре. Основное отличие заключается в том, что коллекторная машина постоянного тока имеет механический преобразователь частоты – коллектор, а при мощности более 1…1,5 кВт так же и дополнительные полюса (ДП).
На статоре расположены главные полюса (ГП) с катушками обмотки возбуждения (ОВ) и дополнительные полюса. Обмотка якоря состоит из отдельных якорных катушек, включающих в себя несколько секций, концы которых присоединяются к соответствующим коллекторным пластинам. Возможны два основных способа соединения отдельных секций в обмотку: петлевой (рис. 4.1а) и волновой (рис. 4.1б):
а) б)




Рис. 4.1. Простая петлевая (а) и волновая (б) обмотки машины постоянного тока.
Чтобы присоединить следующую секцию обмотки, можно вернуться под исходный полюс; таким путем при поступательном движении вдоль окружности якоря выполняются соединения петлевой обмотки, называемой так же параллельной обмоткой.
Щетки делят петлевую обмотку на столько пар параллельных ветвей (а), сколько машина имеет пар полюсов (p), т.е. при петлевой обмотке

При втором способе образования обмотки – соединяются между собой секции, лежащие под следующими по окружности якоря полюсами, выполняемого при поступательном движении вдоль окружности якоря. Таким образом, выполняется волновая обмотка, называемая так же последовательной обмоткой. Число параллельных ветвей при волновой обмотке равно 2 (2а=2), независимо от числа полюсов машины. Чтобы замкнуть волновую обмотку, т.е. чтобы включить в нее все секции обмотки, нужно несколько раз обойти окружность якоря. Петлевая обмотка замыкается после одного обхода якоря.
Простая волновая обмотка применяется для машин малой и средней мощности (до 500 кВт) при напряжении 110 В и выше.
Простая петлевая обмотка применяется для двухполюсных машин малой мощности (до 1 кВт) и машин свыше 500 кВт.
Характерной особенностью машины постоянного тока является (рис. 4.2):
- постоянство (в пространстве) магнитного потока возбуждения;
- наличие преобразователя переменного тока в постоянный, в коллекторных машинах – это механический преобразователь (коллектор).

Рис. 4.2. Электромагнитная схема машины постоянного тока (а) и схема ее
включения (б).(1- обмотка возбуждения; 2- главный полюс; 3- коллектор; 4-щетки; 5- обмотка якоря).
При вращении обмотки якоря в неподвижном магнитном поле, в ней индуктируется переменная ЭДС, изменяющаяся с частотой:

где
n – скорость вращения якоря.
При вращении якоря между любыми двумя точками обмотки якоря действует переменная ЭДС. Однако между неподвижными контактными щетками действует постоянная по величине и направлению ЭДС E, равная сумме мгновенных значений ЭДС e1 , e2 , e3 и т.д. (рис.4.3), индуктированных во всех последовательно соединенных витках якоря, расположенных между этими щетками.

Е
Рис.4.3. Векторная диаграмма, индуктируемых в якорной обмотке ЭДС.
Зависимость ЭДС Е от магнитного потока машины и скорости вращения якоря имеет вид:


При подключении обмотки якоря к сети с напряжением U, ЭДС Е будет приблизительно равна напряжению U, и скорость вращения ротора:

Следовательно, благодаря наличию коллектора при работе машины постоянного тока в двигательном режиме скорость вращения ротора не связана жестко с частотой сети, как в асинхронных и синхронных машинах, а может изменяться в широких пределах путем изменения напряжения U и магнитного потока Ф.
Ось симметрии, разделяющая полюса машины постоянного тока, называется ее геометрической нейтралью.
При разомкнутой внешней цепи ток в обмотке якоря не будет протекать, т. к. ЭДС, индуктированные в двух частях обмотки якоря, расположенных по обе стороны геометрической нейтрали, направлены встречно и взаимно компенсируются. Для того чтобы подать от обмотки якоря во внешнюю цепь максимальное напряжение, эту цепь нужно присоединить к двум точкам обмотки якоря, между которыми действует наибольшая разность потенциалов.
Такими точками являются а и б, расположенные на геометрической нейтрали, где и следует устанавливать щетки А и В (рис.4.3). При вращении якоря точки а и б смещаются с геометрической нейтрали, но к щеткам будут подходить все новые и новые точки обмотки, между которыми действует ЭДС Е, поэтому ЭДС во внешней цепи будет неизменна по величине и направлению. Для уменьшения пульсаций ЭДС при переходе щеток с одной коллекторной пластины на другую в каждую параллельную ветвь обмотки якоря обычно включается не менее 16 активных проводников.
На якорь, по обмотке которого протекает ток I, действует электромагнитный момент:

При работе машины в двигательном режиме электромагнитный момент является вращающим, а в генераторном режиме – тормозным.
Реакция якоря машины постоянного тока
При холостом ходе магнитный поток в машине создается только НС


При работе машины под нагрузкой по обмотке якоря проходит ток, и НС якоря создает свое магнитное поле. Воздействие поля якоря на магнитное поле машины называют реакцией якоря. Магнитный поток Фaq , созданный НС якоря Faq в двухполюсной машине при установке щеток на нейтрали направлен по поперечной оси машины, поэтому магнитное поле якоря называют поперечным. В результате действия потока Фaq симметричное распределение магнитного поля машины искажается, и результирующий поток Фрез оказывается сосредоточенным в основном у краев главных полюсов. При этом физическая нейтраль б-б (линия, соединяющая точки окружности якоря, в которых индукция равна нулю) смещается относительно геометрической нейтрали а-а на некоторый угол ? (рис.4.4). В генераторах физическая нейтраль смещается по направлению вращения якоря; в двигателях – против направления вращения.
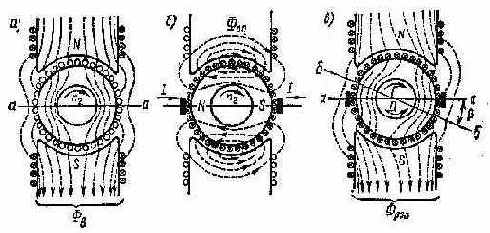
Рис. 4.4. Магнитное поле машины постоянного тока: от обмотки возбуждения (а), от обмотки якоря (б) и результирующее (в).
Вследствие сосредоточенного характера обмотки возбуждения, кривая распределения создаваемой ею НС



Рис.4.5. Распределение индукции в воздушном зазоре машины постоянного тока: от обмотки возбуждения (а), от обмотки якоря (б) и результирующее (в).
На основании закона полного тока НС якоря, действующая в воздушном зазоре на расстоянии x от оси главных полюсов определится выражением:

Следовательно, НС якоря Faq изменяется линейно вдоль его окружности; под серединой главного полюса она равна нулю, а в точках, где установлены щетки, имеет максимальное значение. Магнитная индукция в воздушном зазоре при ненасыщенной магнитной системе:

где

Из последнего выражения следует, что под полюсом при





Реакция якоря оказывает неблагоприятное влияние на работу машины постоянного тока:
а)- физическая нейтраль смещается относительно геометрической нейтрали на некоторый угол, что ухудшает коммутацию коллекторной машины;
б)- результирующий магнитный поток машины при насыщенной магнитной цепи уменьшается, а значит, уменьшается ЭДС Е, индуктированная в обмотке якоря при нагрузке, по сравнению с ЭДС Е0 при холостом ходе;
в)- в кривой распределения индукции

4.3. Коммутация в коллекторных машинах постоянного тока
Необходимым условием долговечности коллекторной машины постоянного тока является отсутствие искрения под щетками, так как искры быстро разрушают пластины коллектора и щетки.
Причины искрения могут быть механическими и электрическими. Основная механическая причина искрения – это ухудшение контакта между коллектором и щетками.
Электрической причиной является неудовлетворительная коммутация. Коммутацией в электрических машинах называется совокупность явлений происходящих при изменении направления тока в секциях обмотки якоря во время замыкания щетками этой секции накоротко.
Время, в течение которого секция обмотки вращающегося якоря замкнута щеткой накоротко, называется периодом коммутации:

где
вщ – ширина щетки;
Vk – окружная скорость коллектора.
Если бы в коммутируемой секции не индуктировалось ЭДС, то ход процесса коммутации тока в секции определялся бы только соотношением сопротивлений контактов щетки с двумя пластинами коллектора (рис.4.6).

Рис. 4.6. К расчету коммутационного процесса в коммутируемой секции якоря.
Будем считать, что ширина щетки не больше ширины одной коллекторной пластины и пренебрегать относительно небольшими сопротивлениями проводников, соединяющих обмотку якоря с коллектором, и самой секции, по сравнению с переходным сопротивлением rщ контакта щетки и коллектора.
Переходное сопротивление r1 контакта с пластиной, уходящей из-под щетки, должно возрастать во время коммутации, достигая бесконечности в конце периода коммутации:
r1=rщ


где
T- период коммутации;
t – время, прошедшее с момента начала коммутации.
В то же время переходное сопротивление контакта со второй пластиной уменьшается:

Ток I, поступающий в щетку из обмотки якоря, должен распределиться между двумя пластинами коллектора обратно пропорционально их переходным сопротивлениям:

С другой стороны, согласно первому закону Кирхгофа:

Решив эту систему уравнений, найдем ток в коммутируемой секции:

В начальный момент времени при t=0 этот ток


Ток I является током лишь одной параллельной ветви обмотки якоря; в общем случае при 2а параллельных ветвей, ток якоря

Следовательно, в общем случае

Такая коммутация называется прямолинейной или равномерной (рис. 4.7а). В этом идеальном случае плотность тока под всей щеткой неизменна во все время коммутации, благодаря чему отсутствуют коммутационные причины искрения.
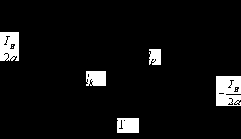



Рис. 4.7. Законы изменения тока коммутируемой секции якоря при линейной (а) и нелинейной (б) коммутации.
Мы рассмотрели идеальный случай. В реальных условиях неизбежно возникают ЭДС самоиндукции в коммутирующей секции lL и ЭДС взаимоиндукции


Её можно выразить следующим образом:

Реактивная ЭДС задерживает изменение тока (рис. 4.7б) и делает коммутацию замедленной в течение большей части периода, но к концу периода, когда уходящая пластина выйдет из-под щетки, ток в секции принудительно примет значение

Для того, чтобы скомпенсировать действие реактивной ЭДС, необходимо противопоставить ей вторую ЭДС, называемую коммутирующей ЭДС


Коммутирующая ЭДС создается посредством движения витков коммутируемой секции во внешнем магнитном поле. В большинстве случаев ek индуктируется магнитным полем дополнительных полюсов машины Фд.п. . Следовательно,

При изменениях нагрузки изменяется реактивная ЭДС, пропорциональная току якоря, но одновременно в такой же мере меняется и коммутирующая ЭДС, т. к. обмотка дополнительных полюсов соединена последовательно с якорем.
Усилив поле дополнительных полюсов путем увеличения числа витков их обмотки, можно сделать

В машинах малой мощности для создания коммутирующего магнитного поля вместо дополнительных полюсов применяется сдвиг щеток с геометрической нейтрали. При таком сдвиге в коммутируемой секции ЭДС

Особо опасный случай неблагоприятной коммутации представляет собой круговой огонь по коллектору. Это – мощная электрическая дуга, замыкающаяся непосредственно по коллектору или даже перекидывающаяся на станину машины, при этом повреждение машины может быть весьма значительным. Круговой огонь возникает при резком броске тока якоря, что вызывает увеличение реактивной ЭДС, а она создает мощную дугу между щеткой и краем уходящей пластины. Эта дуга удерживается и растягивается вследствие вращения коллектора; в результате возникает короткое замыкание непосредственно на коллекторе машины, разрушающее коллектор и щетки.
4.4. Генераторы постоянного тока
В зависимости от способа питания обмотки возбуждения различают генераторы:
- с независимым возбуждением;
- с параллельным возбуждением;
- с последовательным возбуждением (сериесный);
- со смешанным возбуждением (компаундный); он имеет две обмотки возбуждения; одна включена параллельно обмотке якоря, а другая - последовательно с нею и нагрузкой.
Генераторы малой мощности иногда выполняются с постоянными магнитами. Свойства таких генераторов близки к свойствам генераторов с независимым возбуждением.
В генераторе с независимым возбуждением (рис. 4.8а) ток возбуждения

Основными характеристиками генератора являются характеристики: холостого хода, внешняя, регулировочная и нагрузочная.
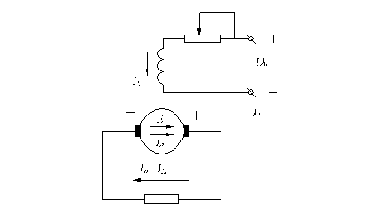

Рис. 4.8. Принципиальная схема генератора с независимым возбуждением (а) и его характеристика холостого хода (б).
Характеристика холостого хода U0=f(Iв) при Iн=0 и n=const (рис. 4.8б). Расхождение входящей и нисходящей ветвей характеристики объясняется наличием гистерезиса в магнитопроводе машины. Eост составляет 2…4 % от Uном.
а) б)

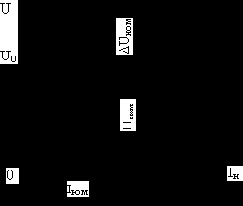
Рис. 4.9. Внешняя (а) и регулировочная (б) характеристики генератора с независимым возбуждением.
Внешней характеристикой называется зависимость U=f(Iн) при n=const и Iн=const (рис. 4.9а). Под нагрузкой напряжение генератора

где
?r – сумма сопротивлений всех обмоток, включенных последовательно в цепь якоря (якоря, дополнительных полюсов и компенсационной обмотки).
С увеличением нагрузки напряжение U уменьшается по двум причинам:
- из-за падения напряжения во внутреннем сопротивлении ?r машины;
- из-за уменьшения ЭДС E в результате размагничивающего действия реакции якоря.
Величина

В генераторе с параллельным возбуждением (рис. 4.10а) обмотка возбуждения присоединена через регулировочный реостат параллельно обмотке якоря. Для нормальной работы приемников электроэнергии необходимо поддерживать постоянство напряжения на их зажимах, несмотря на изменение общей нагрузки генератора. Это осуществляется посредством регулирования тока возбуждения.
Регулировочной характеристикой генератора (рис. 4.9б) называется зависимость тока возбуждения Iв от тока якоря Iа при постоянном напряжении U и скорости n. Такая характеристика показывает, как надо изменять ток возбуждения для того, чтобы при изменениях нагрузки поддерживать постоянство напряжения на зажимах генератора. Эта кривая сначала почти прямолинейна, но затем загибается вверх от оси абсцисс, вследствие влияния насыщения магнитопровода машины. Следовательно, в машине используется принцип самовозбуждения, при котором обмотка возбуждения получает питание непосредственно от самого генератора.

а)

б)
Рис. 4.10. Принципиальная схема генератора с параллельным возбуждением (а); характер изменения ЭДС и тока возбуждения генератора в процессе возбуждения (б).
Самовозбуждение генератора возможно только при наличии гистерезиса в магнитной цепи.
При вращении якоря в его обмотке потоком остаточного магнетизма индуктируется ЭДС Еост , и по обмотке возбуждения начинает протекать ток. Если обмотка возбуждения включена так, что ее НС Fв направлена согласно с НС остаточного магнетизма, то магнитный поток возрастает, увеличивая ЭДС Е, поток Ф и ток возбуждения Iв. Машина самовозбуждается и начинает устойчиво работать с Iв=const, E=const, зависящими от величины сопротивления Rв цепи возбуждения.
Для режима холостого хода генератора:

где
L – суммарная индуктивность обмоток возбуждения и якоря.
Зависимость e=f(iв) представляет собой характеристику холостого хода генератора ОА, а прямая ОВ – ВАХ сопротивления Rв (tg?= Rв) (рис. 4.10б).
Пока имеется положительная разность (e-iвRв), член


Степень устойчивости рассматриваемого режима будет определяться производной:

где
? – угол пересечения характеристики ОА с прямой ОВ.
При увеличении Rв до критического значения Rв.кр., соответствующего ?кр , угол ??0 и режим самовозбуждения становится неустойчивым, при этом ЭДС генератора уменьшается до Еост. Таким образом, для нормальной работы генератора с параллельным возбуждением необходимо, чтобы Rв<Rв.кр.
Внешняя характеристика генератора с самовозбуждением располагается ниже внешней характеристики генератора с независимым возбуждением (рис. 4.11).
Объясняется это тем, что в рассматриваемом генераторе напряжение уменьшается не только с ростом нагрузки и размагничивающего действия реакции якоря, но и вследствие уменьшения тока возбуждения

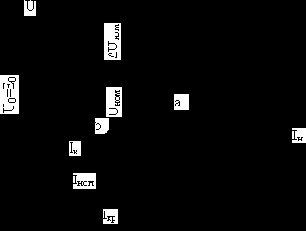 |
Рис. 4.11. Внешние характеристики генераторов с независимым (верхняя кривая) и параллельным (нижняя кривая) возбуждением.
Ток короткого замыкания создается только ЭДС от остаточного магнетизма и составляет (0,4…0,8) Iном.
Работа на участке ab внешней характеристики неустойчива.
Регулировочная характеристика генератора с параллельным возбуждением имеет такой же вид, как и для генератора с независимым возбуждением.
В генераторе с последовательным возбуждением (рис. 4.12а) ток возбуждения Iв=Iа=Iн.
а) б)
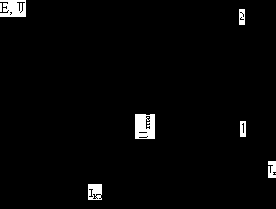

Рис. 4.12. Схема генератора с последовательным возбуждением (а) и его внешняя характеристика (б).
Внешняя характеристика (кривая 1) и характеристика холостого хода (кривая 2) изображены на рис. 4.12б. Ввиду того, что в генераторе с последовательным возбуждением напряжение сильно изменяется при изменении нагрузки, такие генераторы практически не применяются. Их используют лишь при электрическом торможении двигателей с последовательным возбуждением, которые при этом переводятся в генераторный режим.
В генераторе со смешанным возбуждением имеются две обмотки возбуждения: основная (параллельная) и вспомогательная (последовательная). Наличие двух обмоток при их согласном включении позволяет получать приблизительно постоянное напряжение генератора при изменении нагрузки. Подбирая число витков последовательной обмотки так, чтобы при номинальной нагрузке создаваемое ею напряжение ?Uпосл компенсировало суммарное падение напряжения ?U при работе машины с одной только параллельной обмоткой, можно добиться, чтобы напряжение U при изменении тока нагрузки от нуля до Iном оставалось практически неизменным.
Генераторы постоянного тока имеют большей частью параллельное возбуждение. Обычно для улучшения внешней характеристики они снабжаются небольшой последовательной обмоткой (1-3 витка на полюс). При необходимости такие генераторы могут включаться и по схеме с независимым возбуждением.
Генераторы с независимым возбуждением используются только при большой мощности и низком напряжении. В этих машинах независимо от величины напряжения на якоре обмотка возбуждения рассчитывается на стандартное напряжение постоянного тока 110 или 220 В с целью упрощения регулирующей аппаратуры.
4.5. Двигатели постоянного тока
Так же как и генераторы, двигатели классифицируются по типу возбуждения: с параллельным (шунтовые), последовательным (сериесные) и смешанным (компаундные) возбуждением.
При работе машины постоянного тока в двигательном режиме U>E, поэтому


В двигателе с параллельным возбуждением (рис. 4.13а) обмотка возбуждения подключена параллельно с обмоткой якоря к сети.


0
Рис. 4.13. Схема двигателя с параллельным возбуждением (а) и его механические характеристики (б).
Если пренебречь размагничивающим действием реакции якоря, то можно считать, что магнитный поток двигателя не зависит от тока нагрузки. В этом случае механическая характеристика двигателя ?=f(M) будет линейной.

где


Сумма сопротивлений (

В этом случае они называются естественными характеристиками. При включении добавочного сопротивления rn угол наклона этих характеристик возрастает, вследствие чего можно получить семейство реостатных характеристик 2,3,4, соответствующих различным значениям rn (рис. 4.13б). Чем больше rn , тем больший угол наклона имеет реостатная характеристика, т. е. тем она мягче. Современные двигатели с параллельным возбуждением снабжаются небольшой последовательной обмоткой возбуждения, которая передает механической характеристике необходимый угол наклона. НС этой обмотки при токе Iном составляет до 10 % от НС параллельной обмотки.
Регулировочный реостат rр.в позволяет изменять ток возбуждения двигателя Iв и тем самым его магнитный поток. Согласно выражению ?=f(Ф) при этом будет изменяться и скорость вращения двигателя. В цепь обмотки возбуждения никаких выключателей и предохранителей не устанавливают, т.к. при разрыве этой цепи и небольшой нагрузке на валу скорость двигателя резко возрастает (он идет в «разнос»). При этом сильно увеличивается ток якоря и возникает круговой огонь на коллекторе машины.
В двигателе с последовательным возбуждением (рис. 4.14а) ток возбуждения равен току якоря: Iв=Iа , поэтому магнитный поток Ф является функцией тока нагрузки Iа. Характер этой функции изменяется в зависимости от величины нагрузки. При Ia<(0,8…0,9) Iном, когда магнитная система ненасыщенна, Ф=кфIа , причем коэффициент пропорциональности Кф в значительном диапазоне нагрузок остается практически постоянным. При дальнейшем возрастании нагрузки поток Ф растет медленнее, чем Ia , и при больших нагрузках (Ia>Iном) можно считать, что Ф=const. В соответствии с этим изменяются и зависимости n=f(Ia), M=f(Ia) (рис. 4.14б).
а) б)


Рис.4.14. Схема двигателя с последовательным возбуждением (а) и зависимости его момента и скорости вращения от тока якоря (б).


Кроме естественных характеристик 1, можно путем включения добавочных сопротивлений rn в цепь якоря получить семейство реостатных характеристик 2, 3, и 4. Чем больше величина rn, тем ниже располагается характеристика.
При малых нагрузках скорость n резко возрастает и может превысить максимально допустимое значение (двигатель идет в «разнос»). Поэтому такие двигатели нельзя применять для привода механизмов, работающих в режиме холостого хода и при небольшой нагрузке. Обычно минимально допустимая нагрузка составляет (0,2…0,25) Iном; только двигатели малой мощности (десятки ватт) используют для работы при холостом ходе. Применение ременной передачи или фрикционной муфты для включения недопустимо.
Двигатели с последовательным возбуждением применяют в тех случаях, когда имеет место изменение нагрузочного момента в широких пределах и тяжелые условия труда.
При жесткой характеристике скорость вращения n почти не зависит от момента М, поэтому мощность:

где С4 – постоянная.
При мягкой характеристике двигателя n обратно пропорционально


где

Поэтому при изменении нагрузочного момента в широких пределах мощность Р2 , а, следовательно, мощность Р1 и ток Ia изменяются у двигателей с последовательным возбуждением в меньших пределах, чем у двигателя с параллельным возбуждением, кроме того, они лучше переносят перегрузки.
В двигателе со смешанным возбуждением магнитный поток Ф создается в результате совместного действия двух обмоток возбуждения - параллельной и последовательной. Поэтому его механическая характеристика располагается между характеристиками двигателей с параллельным и последовательным возбуждением (рис. 4.15).
Достоинством двигателя со смешанным возбуждением является то, что он, обладая мягкой механической характеристикой, может работать при холостом ходе, так как его скорость холостого хода n0 имеет конечное значение.
 |
Рис.4.15. Механические характеристики двигателя со смешанным возбуждением.
5. Информационные машины
К числу информационных машин относятся: поворотные трансформаторы, сельсины, магнесины и асинхронные тахогенераторы.
5.1. Поворотный трансформатор
Поворотными трансформаторами называют электрические машины переменного тока, преобразующие угол поворота ? в напряжение, пропорциональное некоторым функциям этого угла или самому углу. В зависимости от закона изменения выходного напряжения они подразделяются на следующие типы:
а) синусно – косинусный трансформатор, позволяющий получить на выходе два напряжения, одно из которых пропорционально sin?, а второе cos?;
б) линейный поворотный трансформатор, выходное напряжение которого пропорционально углу ?;
в) трансформатор – графопостроитель, выходное напряжение которого связано с подаваемыми первичными напряжениями зависимостью:

где
С – постоянная.
Для получения поворотных трансформаторов различных типов может быть использована одна и та же машина с двумя обмотками на статоре и двумя на роторе при различных способах включения обмоток.
Поворотные трансформаторы широко используются в автоматических и вычислительных устройствах для решения геометрических и тригонометрических задач. В системах автоматического регулирования они используются в качестве измерителей рассогласования.
Конструктивно поворотный трансформатор выполняется так же, как асинхронный двигатель с фазным ротором. На статоре и роторе расположены по две одинаковые однофазные распределенные обмотки, сдвинутые между собой в пространстве на 90 градусов. Магнитопровод – шихтованный.
Поворотный трансформатор может работать в режиме поворота ротора или в режиме вращения.
В первом случае положение ротора относительно статора задается поворотным механизмом (рис. 5.1).

Рис. 5.1. Принципиальная схема четырехобмоточного поворотного трансформатора.
В этом режиме одна из статорных обмоток – обмотка возбуждения В – присоединяется к сети переменного тока, а другая – компенсационная или квадратурная обмотка К – подключается к некоторому сопротивлению или замыкается накоротко. В некоторых случаях обе статорные обмотки получают питание от независимых источников переменного напряжения. Обмотка ротора S (синусная) и С (косинусная) присоединяются к контактным кольцам. Для уменьшения числа колец концы двух обмоток объединяются. Применяется так же токосъем с помощью спиральных пружин; в этом случае угол поворота ротора ограничен 1,8…2 оборотами.
При работе в режиме вращения обмотки возбуждения и компенсации с целью уменьшения числа контактных колец размещают на роторе, а синусную и косинусную – на статоре. При этом компенсационная обмотка замыкается накоротко, а выводы обмотки возбуждения подключаются к двум контактным кольцам.
Принцип действия. При подключении обмотки возбуждения В к сети переменного тока в машине возникает продольный магнитный поток Фd, пульсирующий во времени с частотой сети. При холостом ходе в обмотках ротора S и С этот поток будет наводить ЭДС Еs0 и Ec0, частота которых равна частоте сети f1, а действующее значение будет зависеть от положения ротора относительно статора (рис. 5.2а).
а) б)
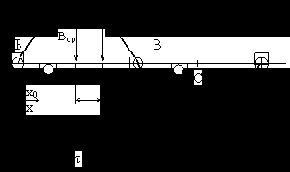 |
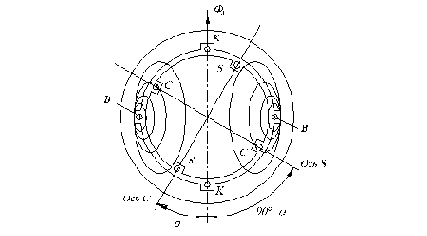
Рис. 5.2. Схематический разрез поворотного трансформатора (а) и график распределения индукции вдоль окружности его статора и ротора (б).
Предположим, что магнитный поток Фd распределен в воздушном зазоре синусоидально; в этом случае индукция в воздушном зазоре изменяется вдоль окружности статора и ротора по закону (рис. 5.2б):

где
Вср – индукция в воздушном зазоре по оси обмотки В.
В обмотке статора В поток Фd индуктирует ЭДС:

где
Фdm – максимальное значение потока:

Здесь
l1 – продольная длина статора (ротора);

Предположим, что ось фазы С обмотки ротора сдвинута относительно фазы В обмотки статора на некоторый угол


а ЭДС, индуцированная в этой обмотке

где

Из соотношения

выходное напряжение косинусной обмотки при холостом ходе

Обмотка ротора S сдвинута относительно обмотки С на угол ?/2 , следовательно, выходное напряжение в этой обмотке

Обмотка К с потоком Фd не связана и он не индуктирует в ней ЭДС. Она используется для компенсации поперечных потоков, создаваемых обмотками ротора при нагрузке поворотного трансформатора. Если вместо обмотки В присоединить к сети переменного тока обмотку К, то она создаст поперченный поток, по отношению к которому обмотка S будет косинусной, а обмотка С – синусной. Таким образом, в обмотках ротора при холостом ходе индуктируются ЭДС, пропорциональные синусу и косинусу угла поворота ротора относительно соответствующего потока. Применяя различные схемы включения обмоток статора и ротора, можно получить и другие функциональные зависимости, а так же уменьшить погрешности, вызываемые током нагрузки.
5.1.1. Синусно – косинусный поворотный трансформатор.
При подключении к синусной обмотке S нагрузки


где

Ток IHS создает НС ротора, максимальное значение которой


Рис. 5.3. Векторная диаграмма НС при подключении нагрузки к синусной обмотке.
Как видно из рис. 5.3 ось этой НС совпадает с осью фазы S, поэтому ее можно представить в виде векторной суммы двух составляющих: продольной Fsd=Fssin? и поперечной Fsq=Fscos?. Продольная составляющая Fsd создает в обмотке возбуждения В компенсирующий ток, НС которого FB , так же, как и в обычном трансформаторе, компенсирует действие Fsd . Результирующий продольный поток Фd индуцирует в обмотке S ЭДС

Поперечная составляющая Fsq создает в поворотном трансформаторе поперечный поток Фq , максимальное значение которого

где

По отношению к поперечному потоку Фq обмотка S является косинусной и, следовательно, в ней индуцируется ЭДС

ЭДС Еsq можно представить в виде:

где

- реактивное сопротивление обмотки ротора.
Таким образом, при нагрузке в синусной обмотке S продольным и поперечным потоками индуктируется результирующая ЭДС

Следовательно, ЭДС, индуцированная в синусной обмотке будет иметь вид:

Решив это уравнение относительно


где

Аналогично можно получить выражение для ЭДС, индуцированной в косинусной обмотке:

где



Таким образом, при наличии тока нагрузки




где




Действительная часть комплексов












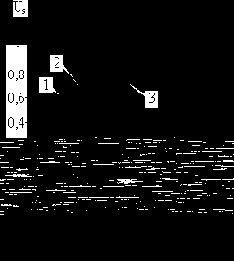 |
Рис. 5.4. Зависимость выходного напряжения









На рис. 5.4 показаны зависимости Us=f(?) при холостом ходе (кривая 1) и при нагрузке (кривые 2 и 3), построенные по вышеуказанным формулам. При этом кривые 2 и 3 соответствуют значениям As, равным 0,25 и 1. Из этих кривых следует, что при нагрузке погрешность поворотного трансформатора может быть весьма значительной. Зависимости амплитудной погрешности ?Us от угла поворота ? для указанных значений модуля комплекса As изображены на рисунке кривыми 4 и 5.
Исследование выражений для


Для устранения погрешности поворотного трансформатора, обусловленной поперечным потоком Фq , применяют так называемое симметрирование трансформатора, т.
е. компенсацию поперечного потока ротора. Существуют два способа симметрирования: вторичное (со стороны ротора) и первичное (со стороны статора).
Вторичное симметрирование. Уменьшить погрешность выходного напряжения, снимаемого с синусной обмотки, можно, если подключить к косинусной обмотке сопротивление

В этом случае ток, проходящий по обмотке С, создает намагничивающую силу, максимальное значение которой

а) б)
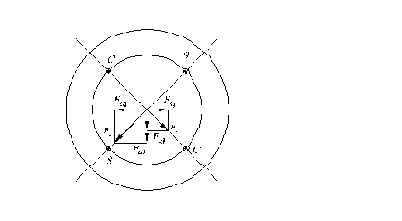

Рис. 5.5. Схема синусно-косинусного трансформатора о вторичным симметрированием (а) и диаграмма МДС, создаваемых обмотками ротора (б).
НС Fc можно представить, как и НС Fs , в виде векторной суммы двух составляющих: продольной Fcd=Fccos? и поперечной Fcq=Fcsin?. Продольная составляющая Fcd совпадает по направлению с Fsd, а поперечная составляющая Fcq направлена против Fsq. При равенстве Fcq =Fsq поперечный поток Фq будет равен нулю. Следовательно, не будет и погрешности, обусловленной этим потоком.
Величину


или

или

Так как поперечный поток Фq равен нулю, то

Следовательно

Откуда

Т.е. при равенстве результирующих сопротивлений обеих фаз ротора ток IB в обмотке возбуждения поворотного трансформатора не зависит от угла поворота ротора, т. к. в выражении для результирующей продольной составляющей НС ротора


или

где


Недостатком этого метода симметрирования является то, что практически он применим только при неизменном сопротивлении нагрузки.
Первичное симметрирование. Если нагрузка подключена только к одной из обмоток ротора, например к обмотке S (рис. 5.6а), то НС ротора по поперечной оси не равна нулю.
а) б)

Рис. 5.6. Схемы синусно – косинусных поворотных трансформаторов с первичным (а) и первичным и вторичным симметрированием (б).
Для уменьшения поперечного потока компенсационную обмотку К статора замыкают на какое-либо малое сопротивление


где

- НС, создаваемая компенсационной обмоткой.
Так как обмотка К по отношению к поперечному потоку Фq представляет собой замкнутую накоротко вторичную обмотку трансформатора, то результирующая НС





при заданном напряжении




Рассмотренные методы компенсации поперечного потока Фq могут быть применены при использовании в качестве рабочей обмотки как синусной, так и косинусной обмоток. Поэтому поворотный трансформатор, подключенный по схеме рис. 5.6б, называют синусно – косинусным.
5.1.2. Линейный поворотный трансформатор
Выбирая определенным образом схемы включения обмоток поворотного трансформатора, можно получить зависимость выходного напряжения от входного угла поворота, в некотором ограниченном диапазоне изменения угла поворота


Диапазон изменения угла




где

Для реализации зависимости (5.1.33) применяют две схемы соединения обмоток поворотного трансформатора: с первичным симметрированием (на статоре) (рис. 5.7а) и с вторичным симметрированием (на роторе) (рис. 5.7б).
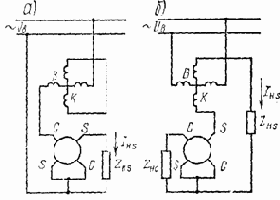
Рис. 5.7. Схема линейного поворотного трансформатора: а) с первичной компенсацией, б) со вторичной компенсацией.
В схеме первичного симметрирования линейного поворотного трансформатора (рис. 5.7а)
компенсационная обмотка замыкается накоротко, поперечный поток при этом равен


Так как ЭДС, индуктированные в косинусной обмотке и обмотке возбуждения совпадают по фазе, то они будут складываться алгебраически.
Поэтому с учетом (5.1.3) и (5.1.6) сумма


Следовательно, согласно (5.1.8) ЭДС, индуктируемая в выходной обмотке S определится выражением:

Пренебрегая падениями напряжения в активных сопротивлениях синусных и косинусных обмоток, а также в активном сопротивлении обмотки возбуждения и принимая

получим окончательное выражение для выходного напряжения линейного поворотного трансформатора:

В линейных поворотных трансформаторах с симметрированием по первичной обмотке изменение нагрузки



В схеме линейного поворотного трансформатора с вторичным симметрированием (рис.5.7б) при изменении нагрузки нарушается условие симметрирования и возникают значительные отклонения от линейной зависимости. Поэтому эту схему применяют сравнительно редко.
5.2. Сельсины
Сельсинами (от слов self sinchroniring – самосинхронизирующийся) называют индукционные машины, обеспечивающие синхронный и синфазный поворот или вращение двух или нескольких осей, механически не связанных между собой. Одна из таких машин механически соединена с ведущей осью и называется датчиком, а другая – с ведомой осью и называется приёмником.
Сельсины имеют две обмотки: возбуждения и синхронизации. Различают одно- и трёхфазные сельсины, обмотка синхронизации у обоих - трехфазная. В системах автоматики наибольшее распространение получили однофазные сельсины, которые бывают контактными и бесконтактными.
Однофазный сельсин представляет собой асинхронную машину, в которой обмотка возбуждения создает пульсирующий поток, индуцирующий в трех фазах обмотки синхронизации ЭДС. Величина этих ЭДС зависит от угла поворота датчика (ротора)

Различают два режима работы сельсинов: индикаторный и трансформаторный.
Индикаторный режим используется при отсутствии другого исполнительного двигателя. Синхронизирующий момент между валами сельсина- датчика и сельсина- приемника создается при наличии некоторого пространственного угла



В трансформаторном режиме к ведомой оси приложен значительный момент сопротивления. Поэтому угол рассогласования

Требования, предъявляемые к сельсинам: статическая и динамическая точность передачи угла; удельный синхронизирующий момент, т.е.
момент, приходящийся на 10 поворота ротора; максимальный синхронизирующий момент при наибольшем угле рассогласования; максимальная скорость вращения сельсинов и время успокоения ротора приемника при скачке поворота ротора датчика.
В зависимости от класса точности статическая ошибка сельсинов составляет ±0,25..2,50.
Устройство сельсинов. Однофазные сельсины, по существу, являются асинхронными машинами малой мощности. Они бывают явнополюсными (индикаторные) и неявнополюсными (трансформаторные). В явнополюсных сельсинах однофазная обмотка возбуждения располагается на явно выраженных полюсах ротора или статора. Обмотка синхронизации всегда выполняется распределенной и располагается в пазах статора или ротора; фазы её соединяются в звезду.
Сельсины выполняются двухполюсными, для того, чтобы обеспечить самосинхронизацию в пределах одного оборота.
Число контактных колец и щеток зависит от места расположения обмоток: сельсины с обмоткой возбуждения на роторе имеют два контактных кольца; с обмоткой возбуждения на статоре – три контактных кольца. В некоторых типах сельсинов применяются электрические или механические демпферы, обеспечивающие быстрое затухание собственных колебаний ротора при переходе его из одного положения в другое.
Для повышения надежности в настоящее время широко применяются бесконтактные сельсины с однофазной обмоткой возбуждения и трехфазной обмоткой синхронизации, расположенными на статоре, вследствие чего отпадает необходимость в скользящих контактах. Недостатком бесконтактных сельсинов является худшее использование материалов из – за больших потоков рассеяния и тока холостого хода. При одинаковых синхронизирующих моментах вес бесконтактного сельсина примерно в 1,5 раза больше, чем контактного.
Трансформаторный режим однофазных сельсинов. Рассмотрим работу однофазных
сельсинов на примере контактных сельсинов с обмоткой возбуждения на статоре. Полученные выводы в одинаковой мере могут быть распространены как на контактные сельсины с обмоткой возбуждения на роторе, так и на бесконтактные сельсины.
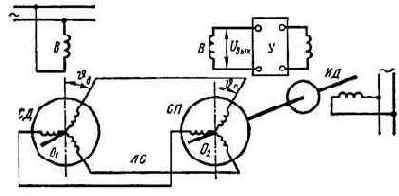
Рис. 5.8. Схема включения сельсинов при работе в трансформаторном режиме.
Переменный ток, проходящий по обмотке возбуждения сельсина- датчика (рис. 5.8), создает в нем пульсирующий магнитный поток, который индуктирует ЭДС в трех фазах обмотки синхронизации. Токи, протекающие от действия этих ЭДС в обмотках синхронизации сельсина – приемника создадут свой пульсирующий магнитный поток. Направление оси этого потока зависит от углового положения ротора приемника. Если при этом в сельсине – приемнике возникает продольная составляющая потока, то она индуцирует в его обмотке возбуждения ЭДС, являющуюся выходным напряжением, подаваемым после усиления на исполнительный двигатель, который поворачивает ведомую ось О2 ротора приемника. Когда ось магнитного потока, создаваемого ротором сельсина – приемника станет перпендикулярной оси обмотки возбуждения, выходное напряжение станет равным нулю и вращение ведомой оси прекратится.
Следовательно, для работы системы необходимо, чтобы ток в роторе сельсина – приемника создавал продольную составляющую магнитного потока. В согласованном положении роторов продольная составляющая магнитного потока сельсина – приемника отсутствует.

Рис. 5.9. Ротор и статор сельсина-датчика при


Обмотка возбуждения В сельсина – датчика создает магнитный поток ФВ, синусоидально распределенный вдоль окружности статора и ротора и пульсирующий с частотой сети. Величина ЭДС, индуктируемая этим потоком, в каждой фазе обмотки ротора датчика зависит от ее положения относительно оси обмотки возбуждения. Если ось первой фазы ротора – датчика совпадает с осью обмотки возбуждения (рис. 5.9а) то

В общем случае, когда ось первой фазы ротора сдвинута относительно обмотки возбуждения на угол


Так как одноименные фазы соединены последовательно, то проходящий по ним ток:

где


Очевидно, что

Считая, что НС отдельных фаз распределены в пространстве синусоидально, получим:

где
F2m=0,9I2mw2 – максимальное значение НС, создаваемой одной фазой обмотки ротора.
Для определения результирующей НС всех трех фаз датчика сложим их составляющие FДd и FДq по продольной оси d (оси обмотки возбуждения) и по поперечной оси q.


Таким образом, результирующая НС ротора датчика может быть представлена пространственным вектором



Намагничивающие силы соответствующих фаз ротора сельсина – приемника будут отличаться от НС фаз ротора датчика только знаком, т. к. ток в фазах обмотки ротора приемника направлен противоположно току в фазах обмотки ротора датчика. Поэтому результирующая НС сельсина – приемника также может быть представлена пространственным вектором


Продольная и поперечная составляющие этой силы:


Знак “-” в этих выражениях указывает, что вектор результирующей НС

поворачивается в противоположную сторону по отношению к НС ротора датчика.

Рис. 5.10. Векторы МДС ротора в датчике



Так как реактивная мощность должна оставаться постоянной, то


Требования, предъявляемые к исполнительным двигателям
Помимо общих требований (предъявляемых ко всем машинам: малые габариты и вес, дешевизна, высокий КПД, надежность и т.д.), к исполнительным двигателям предъявляются и специфические требования: управляемость двигателя при всех режимах работы (отсутствие самохода), линейность механических и регулировочных характеристик, высокое быстродействие, бесшумность работы, малая мощность управления, отсутствие радиопомех и т.д. Эти требования заставляют в ряде случаев отказываться от традиционных конструкций машин общего применения, что ведет к увеличению габаритов, снижению КПД и т.п.
Самоход исполнительных двигателей. Наибольшая асимметрия магнитного поля в исполнительном двигателе будет иметь место при отсутствии напряжения на обмотке управления. При этом режиме коэффициент сигнала

При




В однофазном двигателе общего применения результирующий момент при пуске равен 0, но в довольно широком диапазоне скоростей (при

|
|
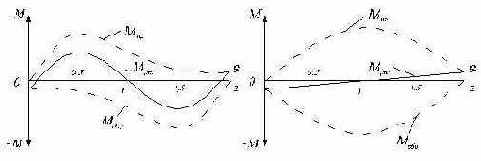
Рис.2.24.Зависимости



Такой двигатель может работать с некоторой установившейся скоростью, если каким-либо образом его предварительно привести во вращение. Однако, использовать такой двигатель в качестве исполнительного невозможно, так как при





Зависимости


Поэтому полученное условие отсутствия самохода можно записать:

Это условие выполняется, если



При изготовлении исполнительных двигателей требуется повышенное внимание к качеству технологических операций, т. к. наличие межвиткового замыкания обмотки статора, а также замыкание между собой пакетов статора может привести к эллиптичности поля машины.
2.4.6. Исполнительный двигатель с амплитудным управлением
Напряжение управления







При амплитудном управлении


Величину

Токи прямой и обратной последовательностей:

.
Аналогично определяются симметричные составляющие тока в фазе управления:



Сопротивления


Рис.2.25. Схема замещения синхронного двигателя для прямой (а) и обратной (б) последовательностей.
Они отличаются величиной активного сопротивления ротора. Сопротивление ротора зависит от скольжения относительно прямого и обратного магнитных полей. Сопротивление ротора для токов прямой последовательности:

Для токов обратной последовательности:

где

- относительная скорость вращения ротора.
Уравнения токов идеализированного двигателя
Воспользуемся упрощенными схемами замещения ротора, в которых пренебрегается индуктивными сопротивлениями рассеяния ротора (рис. 2.26а, б):
|
|

Рис.2.26. Схема замещения идеализированного двигателя для токов прямой (а) и
обратной (б) последовательностей
Основанием для идеализации двигателя является выполнение двигателя с повышенным активным сопротивлением ротора.
Для идеализированного двигателя:

Составляющие тока управления:


Зависимость КПД реального двигателя
из которых следует, что при увеличении относительной скорости


Регулировочные характеристики реального двигателя проходят выше характеристик идеализированного двигателя. Иными словами, при заданном относительном моменте требуемая скорость в реальном двигателе будет достигнута при меньшем коэффициенте сигнала.
Только при малых значениях


Мощности управления и возбуждения у реального двигателя. Ток возбуждения у реального двигателя практически не зависит от режима работы. Поэтому мощность возбуждения





где

Коэффициент мощности имеет максимум при пуске и равен 0,5-0,6 (у двигателя с полнм ротором). С возрастанием скорости



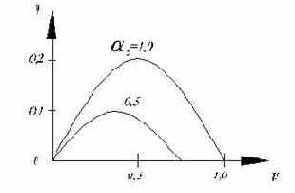
Рис. 2.29. Зависимость КПД реального двигателя с амплитудным управлением от относительной скорости вращения.
С уменьшением коэффициента сигнала


